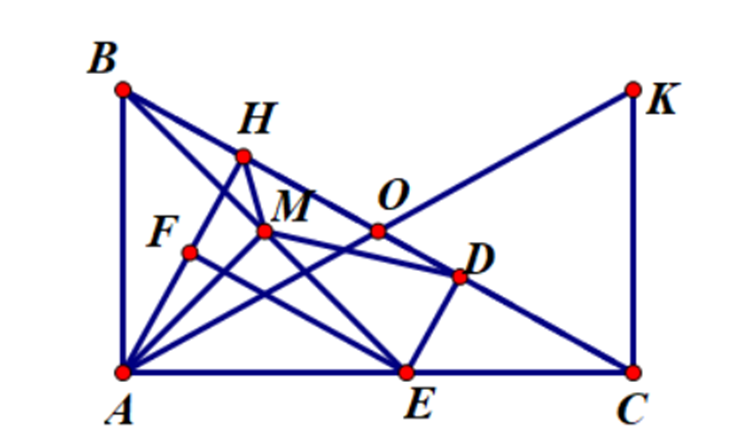
a) Xét tứ giác ABKC có O là trung điểm BC và AK

Suy ra: ABKC là hình bình hành

Mà \(\widehat {BAC} = 90^\circ \)nên ABKC là hình chữ nhật

Do đó: AC = BC; AB = KC

Xét ∆ABC và ∆CKA có:

AB = CK

BC = AK

AC chung

Suy ra: ∆ABC = ∆CKA (c.c.c)

b) Xét tứ giác ABDE có \(\widehat {BDE} + \widehat {ABE} = 90^\circ + 90^\circ = 180^\circ \)

Suy ra: ABDE là tứ giác nội tiếp

Suy ra: \(\widehat {BDA} = \widehat {AEB}\)

Xét tam giác AHD vuông tại H có AH = HD

Suy ra: Tam giác AHD vuông cân tại H ⇒ \(\widehat {HDA} = 45^\circ \)

⇒ \[\widehat {AEB} = 45^\circ \]

Xét tam giác AEB vuông tại A có \[\widehat {AEB} = 45^\circ \]

⇒ \[\widehat {ABE} = 45^\circ \]

⇒ Tam giác AEB vuông cân tại A do đó AB = AE

c) Vì M là trung điểm BE nên ta có: MA = MB = ME (do tam giác ABE vuông tại A nên đường trung tuyến bằng nửa cạnh huyền)

Tương tự trong tam giác BDE vuông tại D có DM là đường trung tuyến

Nên DM = BM = ME

Suy ra: DM = MA = BM = ME

Xét tam giác MHA và tam giác MHD có:

Chung MH

HD = HA (giả thiết)

DM = MA

Suy ra: ∆MHA = ∆MHD (c.c.c)

⇒ \(\widehat {DHM} = \widehat {MHA}\)

Mà \(\widehat {DHM} + \widehat {MHA} = 90^\circ \) nên \(\widehat {DHM} = \widehat {MHA} = 45^\circ \)

Vậy \(\widehat {CHM} = 45^\circ \)

d) S_ABC = \(\frac{1}{2}.AH.BC = \frac{1}{2}.AB.AC\)

⇒ AH.BC = AB.AC

⇒AH².BC² = AB².AC²

⇒ \[\frac{1}{{A{H^2}}} = \frac{{B{C^2}}}{{A{B^2}.A{C^2}}}\]

Mà BC² = AB² + AC² nên:

⇒ \[\frac{{A{C^2} + A{B^2}}}{{A{B^2}.A{C^2}}} = \frac{1}{{A{H^2}}}\]

⇒ \[\frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{A{H^2}}}\].