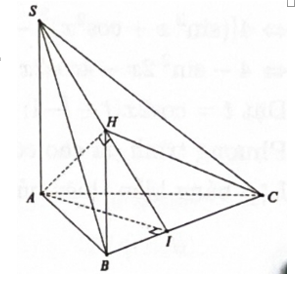
Cho tam giác ABC vuông tại A. Mặt phẳng (P) chứa BC và hợp với mặt phẳng (ABC) góc

Cho tam giác ABC vuông tại A. Mặt phẳng (P) chứa BC và hợp với mặt phẳng (ABC) góc $\alpha$ (0° < a < 90°). Gọi $\beta ,\gamma$ lần lượt là góc hợp bởi hai đường thẳng AB, AC và (P). Tính giá trị biểu thức $P={\cos }^2\alpha +{\sin }^2\beta +{\sin }^2\gamma$

D. P = 1.

Trả lời

Gọi d là đường thẳng vuông góc với (ABC) tại A, S là giao điểm của d và (P)

Khi đó (P) chính là (SBC)

Kẻ $AI\perp BC(I\in BC),AH\perp SI(H\in SI).$

Khi đó $\alpha =\widehat{SIA};\beta =\widehat{ABH};\gamma =\widehat{ACH}.$

$P={\cos }^2\alpha +{\sin }^2\beta +{\sin }^2\gamma =\frac{H{I}^2}{A{I}^2}+\frac{A{H}^2}{A{B}^2}+\frac{A{H}^2}{A{C}^2}$

$=\frac{H{I}^2}{A{I}^2}+A{H}^2\left(\frac{1}{A{B}^2}+\frac{1}{A{C}^2}\right)=\frac{H{I}^2}{A{I}^2}+\frac{A{H}^2}{A{I}^2}=1.$

Chọn D