Cho tam giác ABC vuông tại A. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, d là tiếp tuyến của đường tròn tại A. Các tiếp tuyến của đường tròn tại B và C theo thứ tự ở D và E.
a) Tính \(\widehat {DOE}\).
b) Chứng minh: DE = BD + CE.
c) Chứng minh: BD.CE = R2.
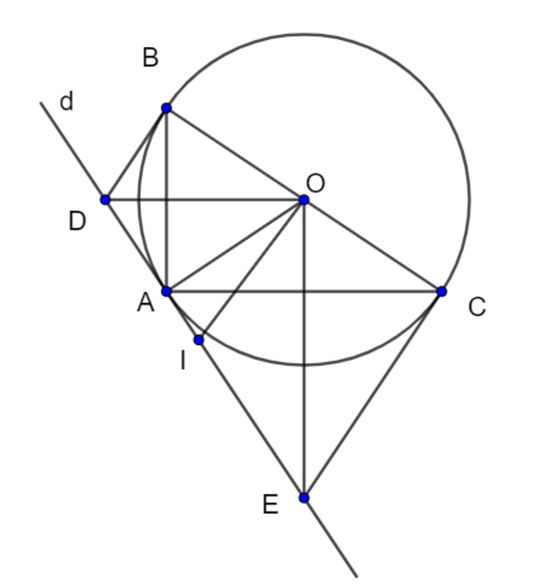
a) Xét (O) có DA, DB là tiếp tuyến cắt nhau tại D
Suy ra: OD là tia phân giác \(\widehat {AOB}\)
⇒ \[\widehat {AOD} = \widehat {BOD}\]
EA, EC là hai tiếp tuyến cắt nhau tại E
⇒ \[\widehat {AOE} = \widehat {COE}\]
⇒ \[\widehat {AOD} + \widehat {AOE} = \widehat {BOD} + \widehat {COE}\]
Mà \[\widehat {AOD} + \widehat {AOE} = \widehat {BOD} + \widehat {COE} = 180^\circ \](kề bù)
Nên \[\widehat {AOD} + \widehat {AOE} = 180^\circ :2 = 90^\circ \]
⇒ \(\widehat {DOE}\)= 90°
b) Xét (O) có DA,DB là hai tiếp tuyến cắt nhau tại D
EA;EC là hai tiếp tuyến cắt nhau tại E
⇒ DA = DB; EA = EC
⇒ BD + CE = DA + EA = DE
c) \(\widehat {DOE}\)= 90° ⇒ Tam giác DOE vuông tại O
DE là tiếp tuyến của (O) nên OA vuông góc DE
Áp dụng hệ thức lượng trong tam giác DOE vuông có OA là đường cao:
OA2 = DA.AE
Mà DA = DB, AE = CE
Nên OA2 = DB.CE = R2
Vậy DB.CE = R2.