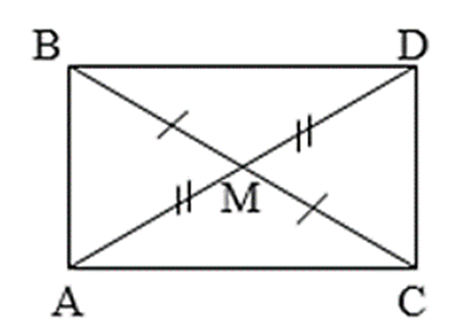
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Chứng minh: ∆MAB = ∆MDC.
b) Chứng minh: AB // CD và ∆ABC = ∆CDA.
c) Chứng minh: ∆BDC là tam giác vuông.
a) Xét ∆MAB và ∆MDC có:
MB = MC (vì M là trung điểm CB)
\(\widehat {BMA} = \widehat {CMD}\)(2 góc đối đỉnh)
MA = MD
Nên: ∆MAB = ∆MDC (c.g.c).
b) Vì ∆MAB = ∆MDC nên \(\widehat {ABC} = \widehat {DCB}\)
Mà 2 góc này ở vị trí so le trong nên AB // CD
Mặt khác: AB vuông góc với AC (do tam giác ABC vuông tại A)
Nên: CD vuông góc với AC
Xét ∆ABC và ∆CDA có:
AB = CD (do ∆MAB = ∆MDC)
\(\widehat {BAC} = \widehat {DCA} = 90^\circ \)
AC chung
Suy ra: ∆ABC = ∆CDA (c.g.c).
c) Xét ∆BDC và ∆CAB có:
AB = CD
\(\widehat {ABC} = \widehat {DCB}\)
BC là cạnh chung
Nên: ∆BDC = ∆CAB (c.g.c)
Suy ra: \(\widehat {BDC} = \widehat {CAB} = 90^\circ \)
Vậy tam giác BDC là tam giác vuông.