Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC còn P, N lần lượt là chân đường vuông góc hạ từ M xuống CA, AB (H.3.60)
477
07/11/2023
Bài 3.44 trang 75 Toán 8 Tập 1: Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC còn P, N lần lượt là chân đường vuông góc hạ từ M xuống CA, AB (H.3.60).
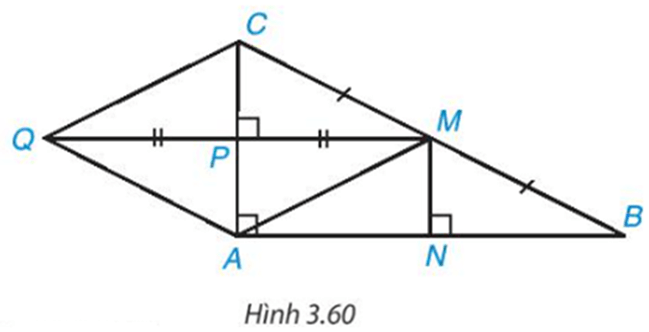
a) Chứng minh hai tam giác vuông CMP và MBN bằng nhau.
b) Chứng minh tứ giác APMN là một hình chữ nhật.
Từ đó suy ra N là trung điểm của AB, P là trung điểm của AC.
c) Lấy điểm Q sao cho P là trung điểm của MQ, chứng minh tứ giác AMCQ là một hình thoi.
d) Nếu AB = AC, tức là tam giác ABC vuông cân tại A thì tứ giác AMCQ có là hình vuông không? Vì sao?
Trả lời
a) Theo đề bài, AC ⊥ MP; AC ⊥ AB.
Suy ra MP // AB nên MP // BN.
Do đó ^CMP=^CBA (hai góc đồng vị).
Ta có P, N lần lượt là chân đường vuông góc hạ từ M xuống CA, AB
Nên ^MPC=^BNM=90° .
Xét ∆CMP và ∆MBN có:
BM = CM (vì M là trung điểm của BC)
(chứng minh trên)
Do đó ∆CMP = ∆MBN (g.c.g).
b) Ta có
Suy ra .
Tứ giác APMN có .
Do đó, tứ giác APMN là một hình chữ nhật.
Suy ra MP = AN; AP = MN (các cặp cạnh tương ứng).
Mà MP = BN; CP = MN (vì ∆CMP = ∆MBN).
Do đó AP = CP; AN = BN.
Từ đó ta suy ra N là trung điểm của AB, P là trung điểm của AC.
c) Tứ giác AMCQ có:
MP = PQ (vì P là trung điểm của MQ)
AP = CP (vì P là trung điểm của AC)
Khi đó, tứ giác AMCQ có hai đường chéo AC và MQ cắt nhau tại trung điểm P của mỗi đường nên nó là hình bình hành.
Mà MQ ⊥ AC.
Do đó tứ giác AMCQ là một hình thoi.
d) Tứ giác APMN là một hình chữ nhật nên MP = AN.
Mà P là trung điểm MQ; N là trung điểm của AB.
Suy ra MQ = AB.
Lại có AB = AC (giả thiết) nên MQ = AC.
Tứ giác AMCQ có hai đường chéo AC và MQ bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm P của mỗi đường.
Do đó, tứ giác AMCQ có là hình vuông.
Xem thêm các bài giải SGK Toán 8 Kết nối tri thức hay, chi tiết khác:

