Cho tam giác ABC vuông tại A. Gọi M là trung điểm của AC , trên tia đối của tia MB
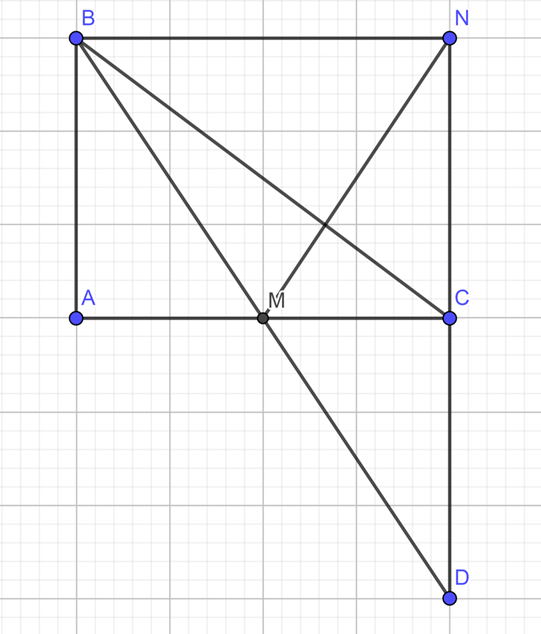
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của AC , trên tia đối của tia MB lấy điểm D sao cho MD =MB.
1) Chứng minh AD = BC.
2) Chứng minh CD vuông góc với AC.
3) Đường thẳng qua B song song với AC cắt tia DC tại N. Chứng minh tam giác ABM = tam giác CNM.