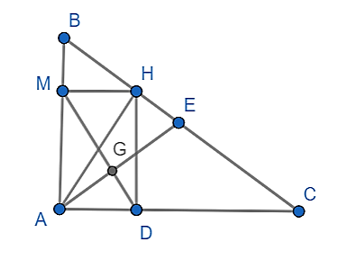
Cho tam giác ABC vuông tại A. Đường cao AH, qua H kẻ HM vuông góc với AB, HD vuông góc với AC. Gọi E là trung điểm BC. Chứng minh AE vuông góc với DM.
51
13/07/2024
Cho tam giác ABC vuông tại A. Đường cao AH, qua H kẻ HM vuông góc với AB, HD vuông góc với AC. Gọi E là trung điểm BC. Chứng minh AE vuông góc với DM.
Trả lời
Xét tam giác ABC vuông tại A có AE là trung tuyến
⇒ AE = EC = BE = ( tính chất trung tuyến ứng với cạnh huyền bằng cạnh huyền)
Suy ra: tam giác AEC cân tại E và
Mà (cùng phụ với )
Nên: = (1)
Xét tứ giác AMHD có:
= 90°
= 90°
Suy ra: AMHD là hình chữ nhật.
Suy ra: (2)
Từ (1) và (2) suy ra: =
Lại có: + = 90°
Nên: + = 90°
Suy ra: = 90° hay MD vuông góc với AE.
Vậy MD vuông góc với AE.