Cho tam giác ABC vuông tại A. Điểm D thuộc cạnh BC. Gọi M, N theo thứ tự là hình chiếu của D tại AB, AC.
17
13/09/2024
Cho tam giác ABC vuông tại A. Điểm D thuộc cạnh BC. Gọi M, N theo thứ tự là hình chiếu của D tại AB, AC.
a) Chứng minh rằng: AD = MN; = 90°.
b) Gọi AH vuông góc BC tại H. Chứng minh rằng: = 90°.
c) Khi D chuyển động trên BC thì trung điểm I của MN chuyển động trên đường nào?
Trả lời
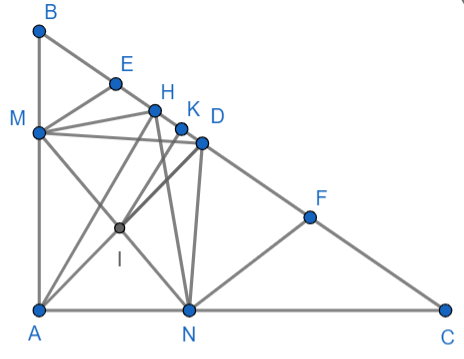
a) Ta có: = 90°
Nên AMDN là hình chữ nhật
Suy ra: AD = MN; = 90°
b) Gọi I là trung điểm của MN và AD
HI là đường trung tuyến của ∆HAD vuông tại H suy ra: HI =
Mà AD = MN nên HI =
Mà HI là đường trung tuyến của ∆HMN (I là trung điểm MN)
Nên ∆HMN vuông tại H
Suy ra: = 90°
c) Kẻ IK vuông góc HD
Ta có: AH ⊥ HD nên IK // AH
Mà I là trung điểm AD nên IK là đường trung bình của tam giác DAH
Suy ra: IK =
Điểm I cách đoạn thẳng BC 1 khoảng cố định bằng một nửa AH không đổi.
Vậy I di chuyển trên đường thẳng song song với BC và cách BC 1 khoảng bằng nửa AH.

