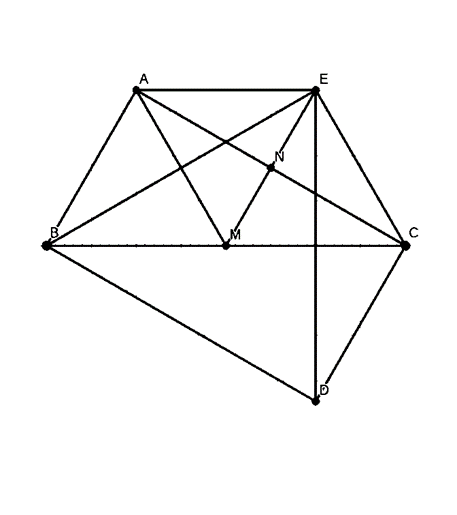
Cho tam giác ABC vuông tại A có \(\widehat C = 30^\circ \). Gọi M và N lần lượt là trung điểm của BC và AC.
a) Tính \(\widehat {NMC}\).
b) Gọi E là điểm đối xứng với M qua N. Chứng minh tứ giác AECM là hình thoi.
c)Lấy D là điểm đối xứng với E qua BC. Tứ giác ACDB là hình gì? Tại sao?
d) Tam giác ABC có điều kiện gì thì tứ giác AECM là hình vuông?
a. Ta có: \(\widehat C = 30^\circ ;\widehat A = 90^\circ \)
Suy ra: \(\widehat B = 90^\circ - \widehat C = 60^\circ \)
Vì M, N là trung điểm BC, AC
⇒ MN // AB
⇒ \(\widehat {NMC} = \widehat B = 60^\circ \)
b. Ta có MN // AB, M là trung điểm BC
⇒ N là trung điểm AC
⇒ ME ⊥ AC = N
⇒ N là trung điểm mỗi đường
⇒ AECM là hình thoi
c. Ta có E,D đối xứng qua BC
⇒ BE = BD, \(\widehat {BCD} = \widehat {ECB}\)
Vì AECM là hình thoi
⇒ \(\widehat {ECB} = 2\widehat {ACB} = 60^\circ \)
⇒ \(\widehat {BCD} = 60^\circ \)
⇒ \(\widehat {ACD} = \widehat {ACB} + \widehat {BCD} = 30^\circ + 60^\circ = 90^\circ \)
⇒ \(\widehat {ACD} = 90^\circ \)
⇒ CD ⊥ AC
⇒ AB // DC vì AB⊥AC
Mà CD = CE = MA = AB (do ΔABM đều)
⇒ ABDC là hình bình hành
Do AC ⊥ CD ⇒ ABDC là hình chữ nhật
d. Để AECM là hình vuông
⇒AM ⊥ MC
⇒ ΔABC vuông cân tại A.