Cho tam giác ABC vuông tại A, có đường cao AH. Từ H kẻ HE vuông góc với AB tại E, HF vuông góc với AC tại F.

a) Cho biết AB = 3cm, $\widehat{ACB}$  = 30°. Tính độ dài các đoạn AC, HA.

b) Chứng minh: BE.BA + CF.CA + 2.HB.HC = BC².

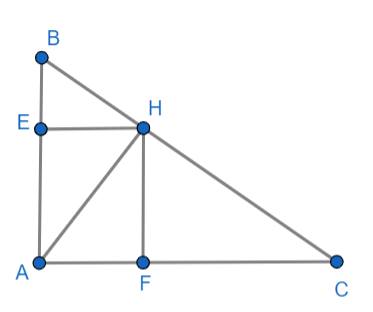
a) Ta có: AB = BC. sin $\widehat{ACB}$

BC = 3 : sin30° = 6(cm)

AC = $\sqrt{B{C}^2-A{B}^2}=\sqrt{6^2-3^2}=3\sqrt{3}$  (cm)

Lại có: S_ABC = $\frac{1}{2}$ AH.BC = $\frac{1}{2}$ AB.AC ⇒ AH = $\frac{AB.AC}{BC}=\frac{3.3\sqrt{3}}{6}=\frac{3\sqrt{3}}{2}$

b) Áp dụng hệ thức lượng trong các tam giác BHA, CHA có:

BE.BA = BH²; CF. CA = HC²

BE.BA + CF.CA + 2.HB.HC = BH² + HC² + 2.HB.HC = (BH + CH)² = BC².

Vậy BE.BA + CF.CA + 2.HB.HC = BC².