Cho tam giác ABC vuông tại A, có AH là đường cao, AM là đường trung tuyến. Qua B kẻ đường thẳng vuông góc với AM tại I cắt AC tại E.

a) Chứng minh BI.BE = 2BH.BM.

b) Chứng minh \(\frac{1}{{A{B^2}}} = \frac{1}{{B{E^2}}} + \frac{1}{{B{C^2}}}\).

Lời giải

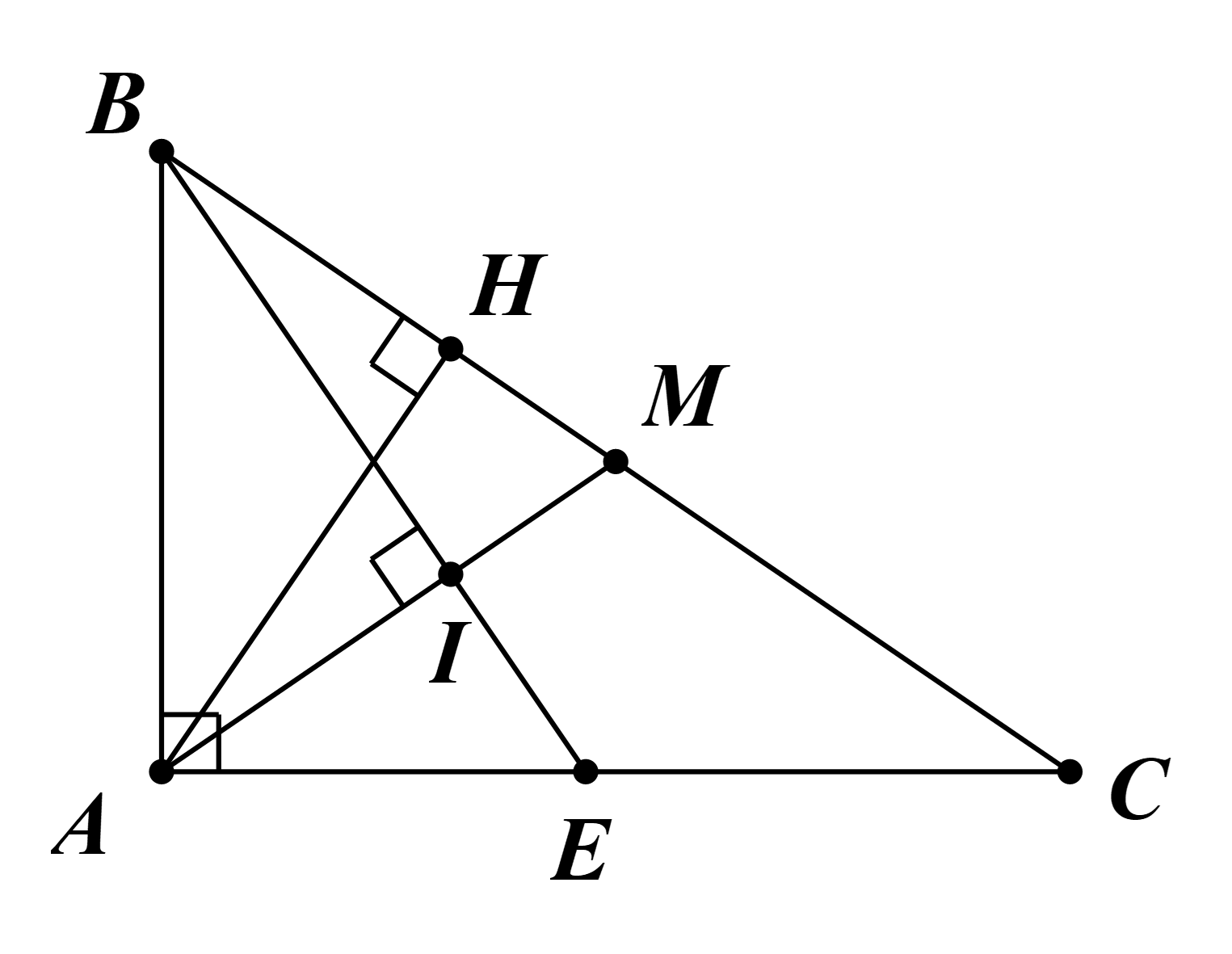
a) Ta có M là trung điểm BC. Suy ra BC = 2BM.

Tam giác ABC vuông tại A có AH là đường cao: AB² = BH.BC = 2BH.BM    (1)

Tam giác ABE vuông tại A có AI là đường cao: AB² = BI.BE     (2)

Từ (1), (2), ta được BI.BE = 2BH.BM.

b) Từ (1), ta có \(BC = \frac{{A{B^2}}}{{BH}}\).

Suy ra \(\frac{1}{{B{C^2}}} = \frac{{B{H^2}}}{{A{B^4}}}\).

Từ (2), ta có \(BE = \frac{{A{B^2}}}{{BI}}\).

Suy ra \(\frac{1}{{B{E^2}}} = \frac{{B{I^2}}}{{A{B^4}}}\).

Xét ∆BMI và ∆AMH, có:

\(\widehat {AMB}\) chung;

\(\widehat {BIM} = \widehat {AHM} = 90^\circ \).

Do đó  (g.g).

Suy ra \(\frac{{BI}}{{AH}} = \frac{{BM}}{{AM}}\).

Mà AM = BM (tam giác ABC vuông tại A có AM là đường trung tuyến).

Do đó BI = AH.

Ta có \(\frac{1}{{B{E^2}}} + \frac{1}{{B{C^2}}} = \frac{{B{I^2}}}{{A{B^4}}} + \frac{{B{H^2}}}{{A{B^4}}} = \frac{{B{I^2} + B{H^2}}}{{A{B^4}}} = \frac{{A{H^2} + B{H^2}}}{{A{B^4}}} = \frac{{A{B^2}}}{{A{B^4}}} = \frac{1}{{A{B^2}}}\).

Vậy ta có điều phải chứng minh.