Cho tam giác ABC vuông tại A, AH là đường cao. Kẻ D đối xứng H qua AB, E đối xứng H qua. Gọi I là giao điểm của AB và DH, K là giao điểm của AC và HE.
a) AIHK là hình gì?
b) D, A, E thẳng hàng.
c) BC = BD + CE.
d) SAIHK = a, tính SDHE theo a.
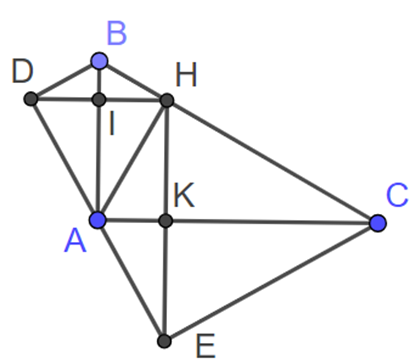
a) H đối xứng D qua AB nên AB là trung trực của HD
⇒ AH = AD và AB vuông góc với HD tại I
⇒ ΔAHD cân tại A
⇒ AB là phân giác của góc HAD(1)
H đối xứng E qua AC nên AC vuông góc với HE tại trung điểm của HE
⇒AC là phân giác của góc HAE(2)
Xét tứ giác AIHK có: \(\widehat {AIH} = \widehat {AKH} = \widehat {KAI}\)= 90°
Nên AIHK là hình chữ nhật
b) Từ (1), (2) suy ra \(\widehat {DAE} = 90^\circ .2 = 180^\circ \)
⇒ D, A, E thẳng hàng
c) Ta có ngay do D, H đối xứng với nhau qua AB nên BH = BD
Tương tự ta có HC = EC
⇒ BD + CE = BH + CH = BC
d) Xét ΔADI và ΔAHI có:
AD = AH (theo a)
Chung AI
DI = HI (do ΔAHD cân tại A)
⇒ ΔADI = ΔAHI (c.c.c)
⇒ SADI = SAHI
Tương tự: SAKH = SAKE
⇒ SAIHK = SDIA + SAKE
Mà SDHE =SAIHK + SDIA + SAKE
Suy ra: SAIHK = \(\frac{1}{2}{S_{DHE}}\)
⇒ SDHE = 2a.