Cho tam giác ABC vuông tại A (AB<AC). Gọi D, E lần lượt là trung điểm của BC, AC. Trên tia đối của tia DE lấy điểm F sao cho D là trung điểm của EF. Vẽ AH vuông góc với BC (H thuộc BC). trên đoạn thẳng HC lấy điểm M sao cho HM = MC. Chứng minh AM vuông góc với FM.

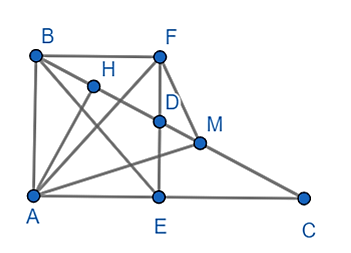
D và E lần lượt là trung điểm của BC và AC nên DE là đường trung bình trong tam giác ABC

Do đó DE // AB; DE = $\frac{1}{2}$ AB

E  và F đối xứng nhau qua D nên D là trung điểm FE

Do đó EF // AB và EF = AB = 2DE

Tứ giác ABFE có: $\left\{\begin{array}{l}EF\parallel AB\\ EF=AB=2DE\end{array}\right.$  và AB ⊥ AE nên ABFE là hình chữ nhật

Gọi I là giao điểm của AF và BE

ABFE là hình chữ nhật nên I là trung điểm của AF và BE và BE = FA

ME là đường trung bình trong ∆AHC nên ME // AH mà AH ⊥ BC ⇒ ME ⊥ BC

∆BME vuông tại M có trung tuyến MI nên MI = $\frac{1}{2}$  BE hay MI = $\frac{1}{2}$ FA

∆FAM có trung tuyến MI và MI =$\frac{1}{2}$ FA nên ∆AFM vuông tại M

Hay AM vuông góc với FM.