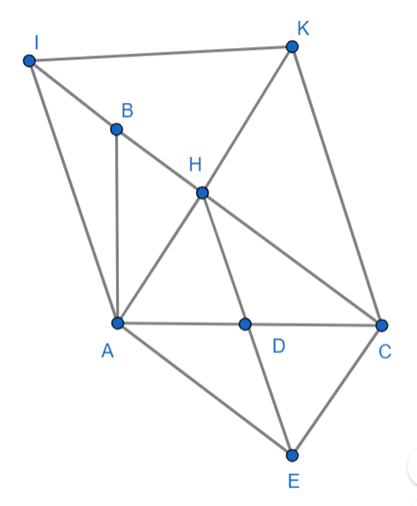
a) Vì E đối xứng với H qua D nên D là trung điểm của HE
Ta có:
Tứ giác AHC có hai đường chéo HE và AC cắt nhau tại trung điểm D của mỗi đường
⇒ AHCE là hình bình hành
Mà AH ⊥ HC
Nên AHCE là hình chữ nhật
b) Vì AHCE là hình chữ nhật
nên AE // HC hay AE // IH
Xét tứ giác AEHI có:
AE // HI
AI // HE
Do đó AEHI là hình bình hành
c) Ta có: AE = HC (AHCE là hình chữ nhật)
mà AE = HI (AEHI là hình bình hành)
⇒ HC = HI
Xét ΔIHA và ΔCHA có:
HI = HC (cmt)
\(\widehat {IHA} = \widehat {CHA}\) (= 90° vì AH là đường cao của Δ ABC)
HA là cạnh chung
⇒ ΔIHA = ΔCHA(c.g.c)
⇒ \(\widehat {HAC} = \widehat {HAI}\) (hai góc tương ứng)
⇒ AK là tia phân giác của \(\widehat {IAC}\)
d) Xét tứ giác CAIK có:
HI = HC(cmt)
AH = HK (gt)
⇒ Hai đường chéo CI và AK cắt nhau tại trung điểm H của mỗi đường
⇒ CAIK là hình bình hành
Hình bình hành CAIK có đường chéo AK là đường phân giác của \(\widehat {IAC}\) (cmt tại câu c )
⇒ CAIK là hình thoi
Hình thoi CAIK là hình vuông (có góc = 90°)
⇒ AK = IC
⇒ AH = HC
⇒ AH vừa là đường cao,đường trung tuyến của ΔABC
⇒ ΔABC là Δ vuông, cân tại A
Hình chữ nhật AHCE có hai cạnh kề bằng nhau ( AH = HC)
⇒ AHCE là hình vuông
Vậy ΔABC là Δ vuông và cân tại A
⇒ Tứ giác CAIK là hình vuông
⇒ Tứ giác AHCE là hình vuông.