Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lấy lần lượt các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM song song với BC (M ∈ AB). Chứng minh tứ giác PCQM là hình chữ nhật.
14
15/08/2024
Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lấy lần lượt các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM song song với BC (M ∈ AB). Chứng minh tứ giác PCQM là hình chữ nhật.
Trả lời
Lời giải
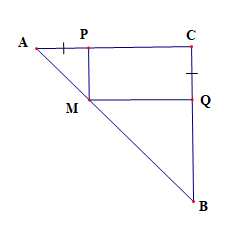
Vì tam giác ABC vuông cân tại C
Nên AC = BC, \(\widehat {CAB} = \widehat {CBA} = 45^\circ \)
Ta có PM // BC và AC ⊥ CB
Suy ra PM ⊥ AC
Do đó tam giác APM vuông tại P
Lại có \(\widehat {PAM} = 45^\circ \)
Suy ra \(\widehat {PAM} = \widehat {PMA} = 45^\circ \)
Do đó tam giác APM vuông cân tại P
Suy ra PA = PM
Mà PA = CQ (giả thiết)
Suy ra PM = CQ
Xét tứ giác PCQM có
PM = CQ
Mà PM // CQ
Suy ra PCQM là hình bình hành
Lại có: \(\widehat C = 90^\circ \)
Suy ra PCQM là hình chữ nhật
Vậy PCQM là hình chữ nhật.

