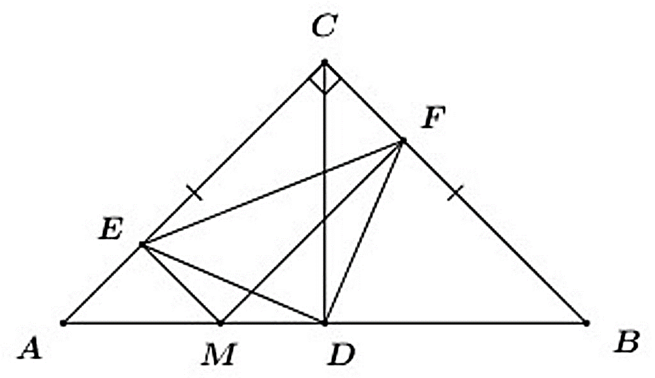
Tam giác ABC vuông cân tại C ⇒ \(\widehat {CBA} = \widehat {CAB} = 45^\circ \)

Xét tam giác AME có: \(\widehat {AEM} = 90^\circ \); \(\widehat {EAM} = \widehat {CAB} = 45^\circ \)

⇒ ΔAME vuông cân tại E ⇒ AE = EM

CMTT ta có tam giác BMF vuông cân tại F ⇒ MF = BF

Xét tứ giác CEMF có \(\widehat {CEM} = \widehat {CFM} = \widehat {ECF} = 90^\circ \)

⇒ CEMF là hình chữ nhật

⇒ EM = CF, MF = CE

⇒ EM = CF = AE, MF = CE = BF

Tam giác ABC vuông cân tại C

⇒ Trung tuyến CD đồng thời là đường cao, phân giác

⇒CD ⊥ AB ⇒\(\widehat {BCD} = 45^\circ \)

Xét ΔAED và ΔCFD có:

AE = CF

AD = CD(tam giác ACD vuông cân tại D)

\(\widehat {DAE} = \widehat {DCF} = 45^\circ \)

⇒ ΔAED = ΔCDF(c.g.c)

⇒ DE = DF(1) (hai cạnh tương ứng) và \(\widehat {ADE} = \widehat {CDF}\) (hai góc tương ứng).

⇒ \(\widehat {ADE} + \widehat {CDE} = \widehat {CDF} + \widehat {CDE}\)

⇒ \(\widehat {ADC} = \widehat {EDF}\)

Mà \(\widehat {ADC} = 90^\circ \)(CD ⊥ AB)

⇒ \(\widehat {EDF} = 90^\circ \)(2)

Từ (1) và (2) suy ra tam giác DEF vuông cân tại D.