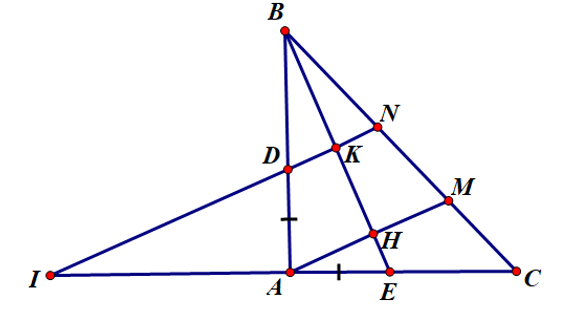
Cho tam giác ABC vuông cân tại A. Trên các cạnh AB, AC lấy tương ứng hai điểm D, E sao cho AD = AE. Từ A và D kẻ đường vuông góc với BE và cắt BC tại M, N. Tia ND cắt tia CA ở I. Chứng minh A
Cho tam giác ABC vuông cân tại A. Trên các cạnh AB, AC lấy tương ứng hai điểm D, E sao cho AD = AE. Từ A và D kẻ đường vuông góc với BE và cắt BC tại M, N. Tia ND cắt tia CA ở I. Chứng minh A là trung điểm của CI.