Cho tam giác ABC vuông cân tại A, đường cao AH. Từ điểm M bất kì trên cạnh BC (M không trùng với B và C) kẻ các đường thẳng song song với AC và AB ở D và cắt AC ở E. Chứng minh \[\widehat {DHE} = 90^\circ \].
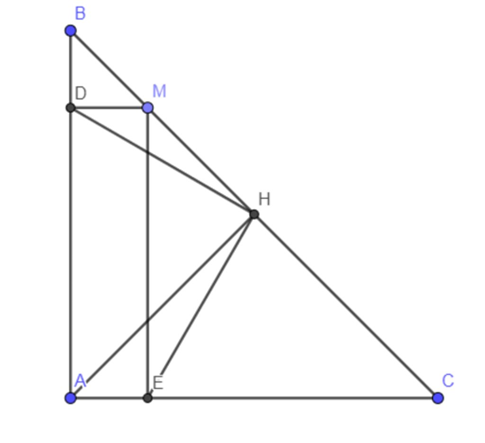
Do ΔABC vuông cân tại A có đường cao AH
⇒ AH = BH = \(\frac{1}{2}BC\)
Ta có
\[\widehat {BMD} = \widehat C\] (2 góc đồng vị)
\[\widehat B = \widehat C\](gt)
⇒ \[\widehat {BMD} = \widehat B\]
Mà MD // AC (gt)
AC ⊥ AB (gt)
⇒ MD ⊥ AB
⇒ \[\widehat {BDM} = 90^\circ \]
Do đó ΔBDM vuông cân tại D
⇒ BD = DM
Lại có tứ giác ADME là hình chữ nhật ( do \[\widehat {BAC} = \widehat {ADM} = \widehat {AEM} = 90^\circ \])
⇒ BD = DM = AE
Mặt khác ta có
\[\widehat {HAC} + \widehat C = 90^\circ \] (ΔACH vuông tại H)
\[\widehat B + \widehat C = 90^\circ \]
⇒ \(\widehat {HAE} = \widehat B\)
Xét ΔHAE và ΔHBD có
HA = HB (cmt)
\(\widehat {HAE} = \widehat B\)(cmt)
AE = BD (cmt)
⇒ ΔHAE = ΔHBD (c.g.c)
⇒ \[\widehat {AHE} = \widehat {BHD}\]
Mà \[\widehat {BHD} + \widehat {AHD} = \widehat {BHA} = 90^\circ \]
⇒ \[\widehat {DHE} = 90^\circ \]