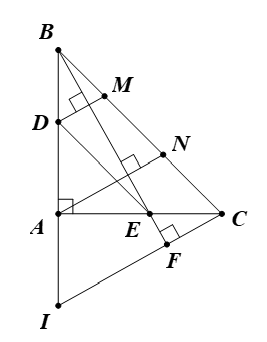
Cho tam giác ABC vuông cân, $\widehat{A}=90°$  . Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Từ C kẻ đường thẳng vuông góc với BE, đường thẳng đó cắt BA tại I.

a) Chứng minh BE = CI.

a)

Gọi F là giao điểm của BE và CI.

Ta có $\widehat{ABE}+\widehat{AEB}=90°$  (∆ABE vuông tại A) và  $\widehat{FCE}+\widehat{CEF}=90°$(∆CEF vuông tại F).

Mà $\widehat{AEB}=\widehat{CEF}$  (cặp góc đối đỉnh).

Suy ra $\widehat{ABE}=\widehat{FCE}$ .

Xét ∆ABE và ∆ACI, có:

AB = AC (∆ABC vuông cân tại A);

$\widehat{ABE}=\widehat{FCE}$ (chứng minh trên);

$\widehat{BAE}=\widehat{CAI}=90°$.

Do đó $\Delta ABE\backsim \Delta ACI$  (g.c.g).

Vậy BE = CI (cặp cạnh tương ứng).