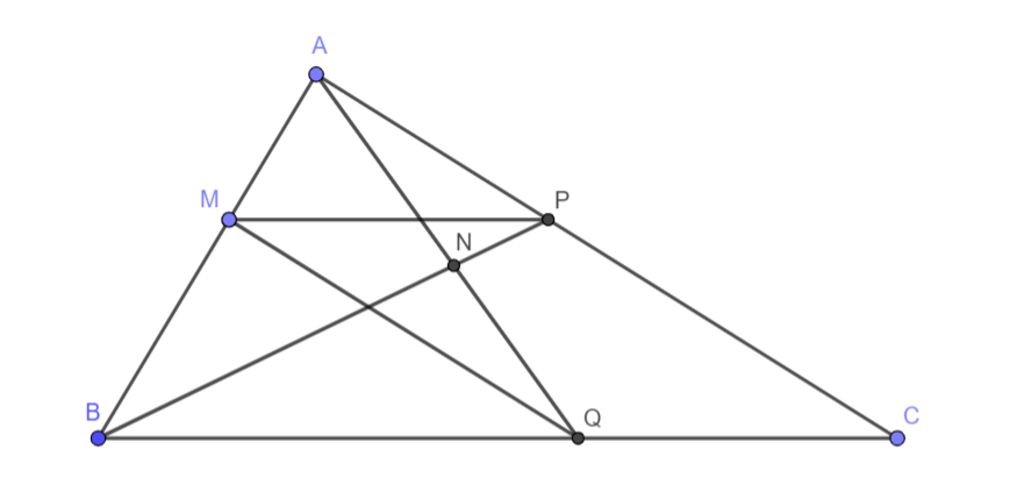
Cho tam giác ABC và điểm M thỏa mãn $3\overrightarrow{MA}+2\overrightarrow{MB}=\overrightarrow{0}$ . Trên các cạnh AC, BC lấy các điểm P, Q sao cho CPMQ là hình bình hành. Lấy điểm N trên AQ sao cho $a\overrightarrow{NA}+b\overrightarrow{NQ}=\overrightarrow{0}$  (với a, b ∈ ℤ và a, b nguyên tố cùng nhau). Khi ba điểm B, N, P thẳng hàng hãy tính a + b.

$\overrightarrow{NP}=\overrightarrow{NA}+\overrightarrow{AP}=\overrightarrow{NA}+\frac{2}{5}\overrightarrow{AC}$

$\overrightarrow{NB}=\overrightarrow{NA}+\overrightarrow{AB}=\overrightarrow{NA}+\frac{5}{2}\overrightarrow{AM}=\overrightarrow{NA}+\frac{5}{2}\left(\overrightarrow{AQ}+\overrightarrow{QM}\right)$

Lại có: $a\overrightarrow{NA}+b\overrightarrow{NQ}=\overrightarrow{0}$  ⇒ $a\overrightarrow{NA}+b\overrightarrow{NA}+b\overrightarrow{AQ}=\overrightarrow{0}$ ⇒ $\overrightarrow{AQ}=\frac{-\left(a+b\right)}{b}\overrightarrow{NA}$

$\overrightarrow{NB}=\overrightarrow{NA}+\frac{5}{2}\overrightarrow{AQ}+\frac{5}{2}\overrightarrow{QM}=\overrightarrow{NA}+\frac{5}{2}.\frac{-\left(a+b\right)}{b}\overrightarrow{NA}+\frac{5}{2}\overrightarrow{CP}$ (CPMQ là hình bình hành)

= $\frac{-5a-3b}{2b}\overrightarrow{NA}+\frac{5}{2}.\frac{3}{5}\overrightarrow{CA}$

= $\frac{-5a-3b}{2b}\overrightarrow{NA}+\frac{3}{2}\overrightarrow{CA}$

B, N, P thẳng hàng nên: $k\overrightarrow{NP}=\overrightarrow{NB}$

⇒ $k\overrightarrow{NA}+\frac{2k}{5}\overrightarrow{AC}=\frac{-5a-3b}{2b}\overrightarrow{NA}-\frac{3}{2}\overrightarrow{AC}$

⇒ $\left\{\begin{array}{l}k=\frac{-5a-3b}{2b}\\ \frac{2k}{5}=\frac{-3}{2}\end{array}\right.$

⇒ $\left\{\begin{array}{l}\frac{15}{4}=\frac{5a+3b}{2b}\\ k=\frac{-15}{4}\end{array}\right.$

⇒ $\left\{\begin{array}{l}30b=4\left(5a+3b\right)=20a+12b\\ k=\frac{-15}{4}\end{array}\right.$

⇒ $\left\{\begin{array}{l}18b=20a\\ k=\frac{-15}{4}\end{array}\right.$

⇒ $\left\{\begin{array}{l}\frac{a}{b}=\frac{9}{10}\\ k=\frac{-15}{4}\end{array}\right.$

Vậy a + b = 19.