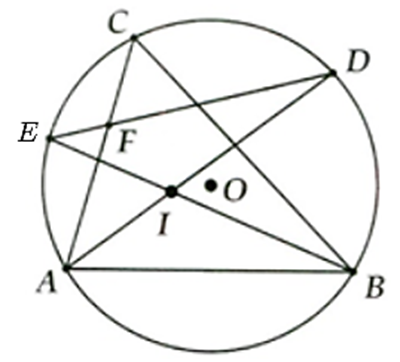
Cho tam giác ABC nội tiếp đường tròn tâm O. Các tia phân giác của các góc A và B cắt nhau ở I và cắt đường tròn theo thứ tự ở D và E. Chứng minh:

a, Tam giác BDI là tam giác cân.

b, DE là đường trung trực của IC.

c, IF và BC song song, trong đó F là giao điểm của DE và AC.