Cho tam giác ABC nội tiếp đường tròn (O), các đường cao AD, BE, CF cắt nhau tại
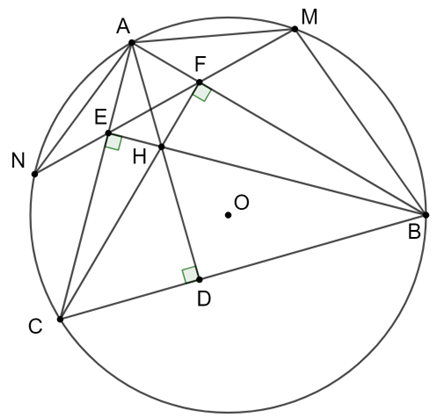
Cho tam giác ABC nội tiếp đường tròn (O), các đường cao AD, BE, CF cắt nhau tại H. Đường thẳng EF cắt đường tròn (O) tại M, N (F nằm giữa M và E). Chứng minh rằng: .
Ta có: \(BE \bot AC \Rightarrow \widehat {BEC} = 90^\circ \) (3)
\(CF \bot AB \Rightarrow \widehat {CFB} = 90^\circ \) (4)
Từ (3) và (4), ta thấy \(\widehat {BEC} = \widehat {CFB} = 90^\circ \)
Vậy tứ giác BFCE nội tiếp.
Khi đó \(\widehat {AFN} = \widehat {ACB}\) (hai góc cùng bù với \(\widehat {BFE}\)) (1)
Mà (tính chất góc nội tiếp trong đường tròn (O)) (2)
(tính chất góc có đỉnh bên trong đường tròn (O)) (3)
Từ (1), (2), (3) suy ra
Do đó .