Câu hỏi:
01/02/2024 100Cho tam giác ABC nhọn, đường cao AH. Lấy điểm D sao cho AB là trung trực của HD. Lấy điểm E sao cho AC là trung trực của HE. Gọi M là giao điểm của DE và AB, gọi N là giao điểm của DE và AC. Khẳng định nào sau đây là đúng?
A. Tam giác ADE cân tại A;
B. HA là tia phân giác của góc MHN;
C. Cả A và B đều đúng;
D. Cả A và B đều sai.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
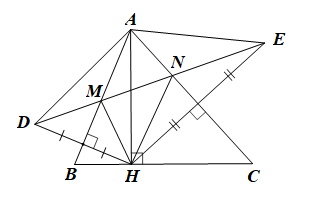
Xét DDHE có AB, AC là hai đường trung trực của tam giác cắt nhau tại A nên A cách đều ba đỉnh của tam giác
Do đó AD = AH = AE.
Tam giác ADE có AD = AE nên là tam giác cân tại A.
Suy ra \(\widehat {ADE} = \widehat {AED}\) (tính chất tam giác cân) (1)
Xét DADM và DAHM có
AM là cạnh chung,
DM = HM (do M thuộc trung trực của DH),
AD = AH (chứng minh trên).
Do đó DADM = DAHM (c.c.c).
Suy ra \(\widehat {ADM} = \widehat {AHM}\)(hai góc tương ứng) (2)
Xét DANH và DANE có
AN là cạnh chung,
NH = NE (do N thuộc trung trực của EH),
AH = AE (chứng minh trên)
Do đó DANH = DANE (c.c.c)
Suy ra \(\widehat {AHN} = \widehat {AEN}\)(hai góc tương ứng) (3)
Từ (1), (2) và (3) suy ra \(\widehat {AHN} = \widehat {AHM}\)
Do đó HA là tia phân giác của góc MHN.
Vậy ta chọn phương án C.
Hướng dẫn giải
Đáp án đúng là: C

Xét DDHE có AB, AC là hai đường trung trực của tam giác cắt nhau tại A nên A cách đều ba đỉnh của tam giác
Do đó AD = AH = AE.
Tam giác ADE có AD = AE nên là tam giác cân tại A.
Suy ra \(\widehat {ADE} = \widehat {AED}\) (tính chất tam giác cân) (1)
Xét DADM và DAHM có
AM là cạnh chung,
DM = HM (do M thuộc trung trực của DH),
AD = AH (chứng minh trên).
Do đó DADM = DAHM (c.c.c).
Suy ra \(\widehat {ADM} = \widehat {AHM}\)(hai góc tương ứng) (2)
Xét DANH và DANE có
AN là cạnh chung,
NH = NE (do N thuộc trung trực của EH),
AH = AE (chứng minh trên)
Do đó DANH = DANE (c.c.c)
Suy ra \(\widehat {AHN} = \widehat {AEN}\)(hai góc tương ứng) (3)
Từ (1), (2) và (3) suy ra \(\widehat {AHN} = \widehat {AHM}\)
Do đó HA là tia phân giác của góc MHN.
Vậy ta chọn phương án C.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba có thể là độ dài ba cạnh của một tam giác là
Câu 2:
Cho tam giác ABC có AH, BK, CL lần lượt là ba đường cao của tam giác ABC. Chọn khẳng định đúng:
Câu 3:
Cho tam giác MNP có trung tuyến MA, NC cắt nhau tại O. Biết MO = 2,5 cm, OC = 1 cm. Độ dài các đường trung tuyến MA, NC lần lượt là:
Câu 5:
Cho tam giác DEF có \(\widehat D = 38^\circ \) và \(\widehat E = 110^\circ .\) Độ dài các cạnh của ∆DEF sắp xếp theo thứ tự tăng dần là
Câu 6:
Cho ∆ABC vuông tại A. Trên cạnh AC lấy điểm M bất kì (M ≠ A, C). Qua M kẻ đường thẳng vuông góc với BC tại N. Từ C kẻ đường thẳng vuông góc với BM tại P. Gọi D là giao điểm của AB và CP. Khẳng định nào sau đây sai?
Câu 7:
Cho tam giác AOM có \(\widehat A = 52^\circ \). Ba đường phân giác cắt nhau tại I. Số đo góc MIO là:
Câu 9:
Cho tam giác ABD có AB < AD < BD và \(\widehat {ADB} = 32^\circ \). Trên cạnh BD lấy điểm C sao cho AB = CA = CB. Số đo của \(\widehat {{\rm{CAD}}}\) là
Câu 11:
Sau khi đo bằng thước đo góc bạn An đã điền số đo các góc vào hai hình vẽ như sau:
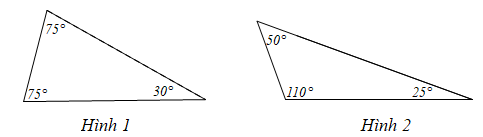
Chọn khẳng định đúng:
Câu 12:
Cho góc nhọn \(\widehat {xOy}\), trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Đường trung trực của OA và đường trung trực của OB cắt nhau tại I.
Cho các khẳng định sau:
(I) OI là tia phân giác của \(\widehat {xOy}\);
(II) OI là đường trung trực của đoạn AB.
Chọn khẳng định đúng:
Câu 13:
Cho tam giác DEF có DM, EN là hai đường trung tuyến cắt nhau tại G. Kéo dài DM lấy điểm H sao cho MH = MD. Kéo dài EN lấy điểm K sao cho NK = NE. Chọn khẳng định sai?
Câu 14:
Cho ∆ABC cân tại A có BC = 9 cm; chu vi ∆ABC bằng 25 cm. Chọn khẳng định sai: