Cho tam giác ABC nhọn, các đường cao AD,BE,CF cắt nhau tại H.

a) Chứng minh: Tam giác ABE và tam giác AFC đồng dạng, AF. AB = AE . AC.

b) Chứng minh $\widehat{AEF}$  = $\widehat{ABC}$ .

c) Cho AE = 3cm, AB = 6cm. Chứng minh: S_ABC = 4S_AEF.

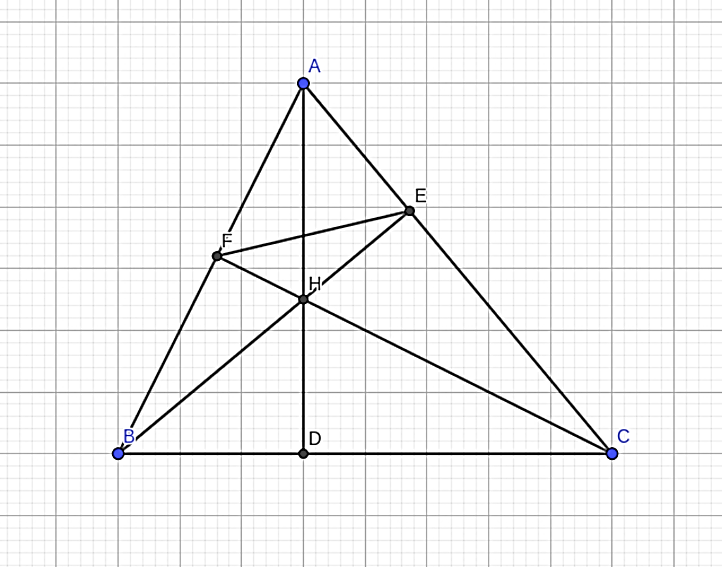
a) Tam giác BAC có BE, CF là đường cao nên CF ⊥ AB, BE ⊥ AC

⇒ $\widehat{AFC}$  = $\widehat{AEB}$  = 90°

Xét ∆ABE và ∆AFC có:

$\widehat{A}$ chung

$\widehat{AFC}$ = $\widehat{AEB}$   = 90°

⇒ ∆ABE ~ ∆AFC (g.g)

⇒ $\frac{AE}{AF}=\frac{AB}{AC}$

⇒ AF.AB = AE.AC

b) Từ $\frac{AE}{AF}=\frac{AB}{AC}$  ⇒ $\frac{AE}{AB}=\frac{AF}{AC}$

Xét ∆AEF và ∆ABC có:

$\widehat{A}$ chung

$\frac{AE}{AB}=\frac{AF}{AC}$

⇒ ∆AEF ~ ∆ABC (c.g.c)

⇒ $\widehat{AEF}$  = $\widehat{ABC}$   (2 góc tương ứng)

c) Ta có: ∆AEF ~ ∆ABC

⇒ $\frac{S_{ABC}}{S_{AEF}}={\left(\frac{AB}{AE}\right)}^2=4$