Cho tam giác ABC, M là trung điểm của AB. Trên tia đối của tia MC lấy điểm N sao cho MC = MN.

a, Chứng minh NB // AC.

b, Trên tia đối tia BN lấy điểm E sao cho BN = BE. Chứng minh: AB = EC.

c, Gọi F là trung điểm của BC. Chứng minh A, E, F thẳng hàng.

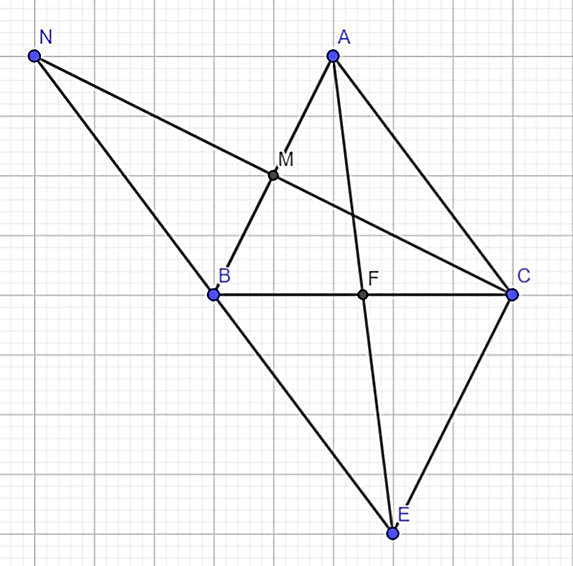
a, Xét ΔMBN và ΔMAC có:

MA = MB vì M là trung điểm BA

$\widehat{NMB}=\widehat{CMA}$(đối đỉnh)
MN = MC

⇒ ΔMNB = ΔMCA(c.g.c)

⇒ $\widehat{MNB}=\widehat{MCA}$

⇒ BN//AC

b, Từ câu a ⇒ AC = BN

Ta có BN // AC ⇒ AC // BE ⇒ $\widehat{AEB}=\widehat{EAC}$

Xét ΔABE và ΔECA có:

Chung AE

$\widehat{AEB}=\widehat{EAC}$

BE = AC

⇒ ΔABE = ΔECA(c.g.c)

⇒ AB = EC

c, Ta có AC // BE ⇒ $\widehat{ACB}=\widehat{CBE}$⇒$\widehat{ACF}=\widehat{FBE}$

Xét ΔACF và ΔBEF có:

FB = FC vì F là trung điểm BC

$\widehat{ACF}=\widehat{FBE}$

AC = BE

⇒ ΔACF = ΔEBF (c.g.c)

⇒ $\widehat{AFC}=\widehat{BFE}$

⇒ A, F, E thẳng hàng.