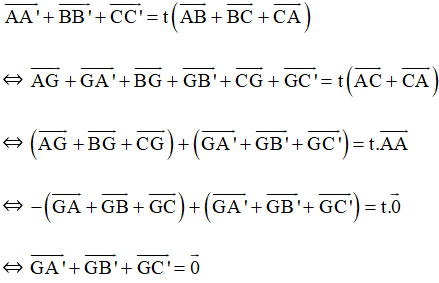Cho tam giác ABC, lấy các điểm A’, B’, C’ không trùng với đỉnh của tam giác và lần lượt

Bài 56* trang 100 SBT Toán 10 Tập 1: Cho tam giác ABC, lấy các điểm A’, B’, C’ không trùng với đỉnh của tam giác và lần lượt thuộc các cạnh AB, BC, CA thỏa mãn $\frac{\text{AA}\text{'}}{AB}=\frac{BB\text{'}}{BC}=\frac{CC\text{'}}{CA}$. Chứng minh hai tam giác ABC và A’B’C’ có cùng trọng tâm.

Trả lời

Đặt $\frac{\text{AA}\text{'}}{AB}=\frac{BB\text{'}}{BC}=\frac{CC\text{'}}{CA}=t$ (t > 0)

⇔ $\left\{\begin{array}{l}AA\text{'}=tAB\\ BB\text{'}=tBC\\ CC\text{'}=tCA\end{array}\right.$

⇒ $\left\{\begin{array}{l}\overrightarrow{AA\text{'}}=t\overrightarrow{AB}\\ \overrightarrow{BB\text{'}}=t\overrightarrow{BC}\\ \overrightarrow{CC\text{'}}=t\overrightarrow{CA}\end{array}\right.$ (vì các điểm A’, B’, C’ lần lượt thuộc các cạnh AB, BC, CA)

Gọi G là trọng tâm tam giác ABC nên $\overrightarrow{\text{GA}}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$

Ta có: 

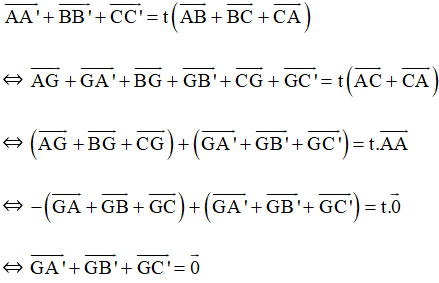
Suy ra G cũng là trọng tâm của tam giác A’B’C’.

Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 3: Khái niệm vectơ

Bài 4: Tổng và hiệu của hai vectơ

Bài 5: Tích của một số với một vectơ

Bài 6: Tích vô hướng của hai vectơ

Bài ôn tập chương 4

Bài 1: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây