Cho tam giác ABC không vuông, với trực tâm H, nội tiếp đường tròn (O). Kẻ đường kính AA' của đường tròn

Bài 4.5 trang 47 SBT Toán 10 Tập 1:

Cho tam giác ABC không vuông, với trực tâm H, nội tiếp đường tròn (O). Kẻ đường kính AA' của đường tròn (O).

a) Chứng minh rằng $\overrightarrow{BH}=\overrightarrow{A^{\text{'}}C}.$ 

b) Gọi M là trung điểm cạnh BC. Tìm mối quan hệ về phương, hướng và độ dài của hai vectơ $\overrightarrow{AH}$và $\overrightarrow{OM}$

Trả lời

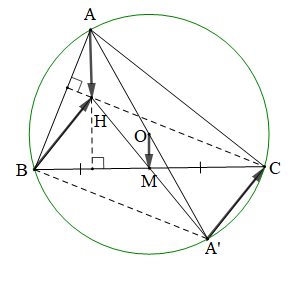
a) Vì H là trực tâm tam giác ABC nên CH ⊥ AB

Mặt khác AA' là đường kính của (O), B ∈ (O) nên $\widehat{AB{A}^{\text{'}}}=90°$ 

Do đó AA' ⊥ AB

Suy ra CH // AA' (từ vuông góc đến song song)

Chứng minh tương tự ta cũng có BH // A'C

Tứ giác BHCA' có CH // AA' và BH // A'C

Suy ra BHCA' là hình bình hành

Do đó $\overrightarrow{BH}=\overrightarrow{A^{\text{'}}C}.$

b) Ta có: O và M lần lượt là trung điểm của AA' và BC

Nên OM là đường trung bình của tam giác AA'H

Do đó AH = 2OM và OM // AH (tính chất đường trung bình)

Vậy, hai vectơ $\overrightarrow{OM}$ và $\overrightarrow{AH}$ có:

+ Cùng phương

+ Cùng hướng

+ $\left|\overrightarrow{AH}\right|=2\left|\overrightarrow{OM}\right|$ 

Xem thêm các bài giải SBT Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 6: Hệ thức lượng trong tam giác

Bài tập cuối chương 3

Bài 7: Các khái niệm mở đầu

Bài 8: Tổng và hiệu của hai vectơ

Bài 9: Tích của một vectơ với một số

Bài 10: Vectơ trong mặt phẳng tọa độ