Cho ba vectơ a,b,c cùng phương và cùng khác vectơ 0 . Chứng minh rằng có ít nhất
Bài 4.3 trang 47 SBT Toán 10 Tập 1: Cho ba vectơ cùng phương và cùng khác vectơ . Chứng minh rằng có ít nhất hai vectơ trong chúng có cùng hướng.
Bài 4.3 trang 47 SBT Toán 10 Tập 1: Cho ba vectơ cùng phương và cùng khác vectơ . Chứng minh rằng có ít nhất hai vectơ trong chúng có cùng hướng.
Ba vectơ cùng phương và cùng khác vectơ nên chúng có thể cùng hướng hoặc ngược hướng nhau.
Trường hợp 1: Nếu cùng hướng với (hoặc cùng hướng với )
Thì khi đó có hai vectơ cùng hướng.
Trường hợp 2: Nếu ngược hướng với cả và
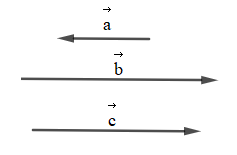
Vì ngược hướng với , ngược hướng với
Nên khi đó và cùng hướng với nhau.
Do đó có hai vectơ trong ba vectơ cùng hướng với nhau
Vậy có ít nhất hai vectơ trong ba vectơ có cùng hướng.
Xem thêm các bài giải SBT Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Bài 6: Hệ thức lượng trong tam giác
Bài 8: Tổng và hiệu của hai vectơ