Cho tam giác ABC, đường trung tuyến AM. Gọi I là điểm bất kì trên đoạn thẳng AM, các tia BI, CI lần lượt cắt các cạnh AC, AB tại D, E. Chứng minh rằng: \(\frac{{AE}}{{AB}} = \frac{{AD}}{{AC}}\).
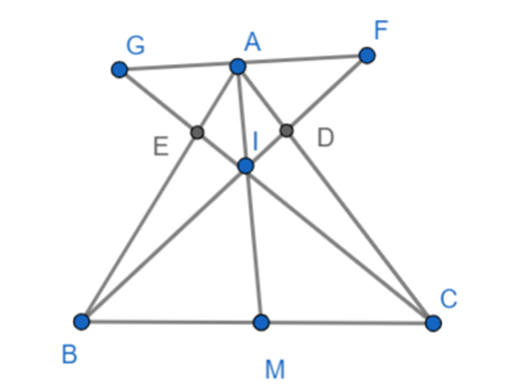
Kẻ BI, CI kéo dài cắt đường thẳng song song với BC qua A tại F, G
Ta có: GA // MC
Áp dụng định lý Ta–let có:
\(\frac{{AG}}{{MC}} = \frac{{IA}}{{IM}}\)(1)
Tương tự: AF // BM nên \(\frac{{AF}}{{BM}} = \frac{{IA}}{{IM}}\) (2)
Từ (1) và (2) suy ra: \(\frac{{AG}}{{MC}} = \frac{{AF}}{{BM}}\)
Mà M là trung điểm BC nên MC = BM
Suy ra: AG = AF
Suy ra: \(\frac{{AG}}{{BC}} = \frac{{AF}}{{BC}}\)
Lại có GA // BC nên \(\frac{{AG}}{{BC}} = \frac{{AE}}{{BE}}\)
AF // BC nên \(\frac{{AF}}{{BC}} = \frac{{AD}}{{DC}}\)
Mà \(\frac{{AG}}{{BC}} = \frac{{AF}}{{BC}}\) nên \(\frac{{AE}}{{BE}} = \frac{{AD}}{{DC}}\)
Suy ra: \(\frac{{AE}}{{BE + AE}} = \frac{{AD}}{{DC + AD}}\)
Hay \(\frac{{AE}}{{AB}} = \frac{{AD}}{{AC}}\)
Vậy \(\frac{{AE}}{{AB}} = \frac{{AD}}{{AC}}\).