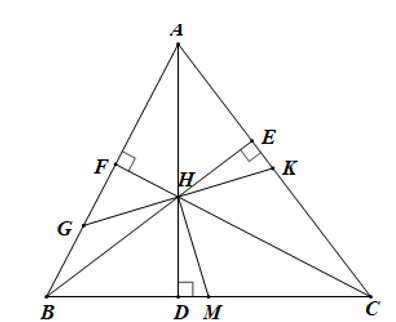
Cho tam giác ABC, đường cao AD, BE, CF cắt nhau tại H. Gọi M là trung điểm của BC, qua H kẻ đường thẳng vuông góc với HM cắt AB, AC lần lượt tại G, K. Chứng minh rằng HG = HK.

Ta có:$\widehat{GHF}+\widehat{HGF}=90°$  (do DGHF vuông tại F) và $\widehat{CHM}+\widehat{CHK}=90°$

Mà $\widehat{GHF}=\widehat{CHK}$   (đối đỉnh) nên $\widehat{HGF}=\widehat{CHM}$  hay $\widehat{HGA}=\widehat{CHM}$

Ta có: $\widehat{BAD}+\widehat{ABD}=90°$  (do DABD vuông tại D);

          $\widehat{BCF}+\widehat{CBF}=90°$  (do DBCF vuông tại F)

Do đó $\widehat{BAD}=\widehat{BCF}$  hay $\widehat{GAH}=\widehat{MCH}$

Xét DGAH và DCHM có: $\widehat{HGA}=\widehat{CHM}$và $\widehat{GAH}=\widehat{MCH}$

Do đó $\Delta GAH \backsim \Delta HCM\left(g.g\right)$

Suy ra $\frac{GH}{HM}=\frac{AH}{CM}$  (tỉ  số đồng dạng) (1)

Tương tự, ta có: $\Delta AHK \backsim \Delta BMH\left(g.g\right)$

Suy ra $\frac{AH}{BM}=\frac{HK}{MH}$  (tỉ số đồng dạng) (2)

Mặt khác: M là trung điểm của BC nên CM = BM (3)

Từ (1), (2) và (3) ta có:$\frac{GH}{HM}=\frac{HK}{MH}$ , suy ra GH = HK.