Cho tam giác ABC đều cạnh bằng 1, trọng tâm G. Tính độ dài vectơ AG
Cho tam giác ABC đều cạnh bằng 1, trọng tâm G. Tính độ dài vectơ \(\overrightarrow {AG} \).
Cho tam giác ABC đều cạnh bằng 1, trọng tâm G. Tính độ dài vectơ \(\overrightarrow {AG} \).
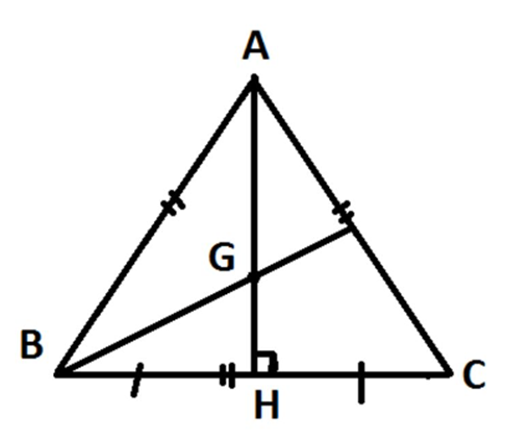
Độ dài của cạnh trong tam giác đều ABC là 1
H là trung điểm cạnh BC
Suy ra: AG = \(\frac{2}{3}AH = \frac{2}{3}\)
Áp dụng định lý Pytago vào tam giác AHC vuông tại H ta có:
\(AH = \sqrt {A{C^2} - H{C^2}} = \sqrt {{1^2} - {{\left( {\frac{1}{2}} \right)}^2}} = \frac{{\sqrt 3 }}{2}\)
Suy ra: AG = \[\frac{2}{3}.\frac{{\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{3}\]
\(\left| {\overrightarrow {AG} } \right| = \frac{{\sqrt 3 }}{3}\).