Cho tam giác ABC đều cạnh a. Tính độ dài các vectơ AB - vectơ AC; vectơ AB  + vectơ AC

Trả lời

Lời giải

Ta có \(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \).

Suy ra \[\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} } \right| = CB = a\].

Gọi M là trung điểm của BC. Suy ra \(BM = \frac{{BC}}{2} = \frac{a}{2}\).

Ta có tam giác ABC đều.

Suy ra AM vừa là đường trung tuyến, vừa là đường cao của tam giác ABC.

Vì vậy \(AM = \sqrt {A{B^2} - B{M^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\).

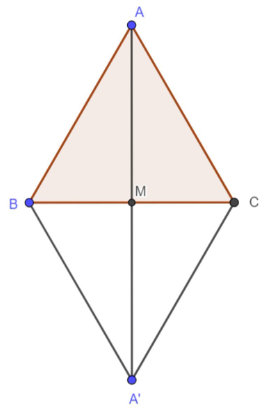
Dựng hình bình hành ABA’C.

Vì M là trung điểm của BC nên M cũng là trung điểm của AA’.

Theo quy tắc hình bình hành, ta có: \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AA'} = 2\overrightarrow {AM} \).

Suy ra \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {2\overrightarrow {AM} } \right| = 2.AM = 2.\frac{{a\sqrt 3 }}{2} = a\sqrt 3 \).

Vậy độ dài các vectơ \(\overrightarrow {AB} - \overrightarrow {AC} ;\overrightarrow {AB} + \overrightarrow {AC} \) lần lượt bằng a và \(a\sqrt 3 \).