Cho tam giác ABC có , và là các góc nhọn, M là một điểm thuộc BC. Gọi D là điểm đối xứng với M qua AB, E là điểm đối xứng với M qua AC. Gọi I, K là giao điểm của DE với AB, AC. a) Tính c
26
12/07/2024
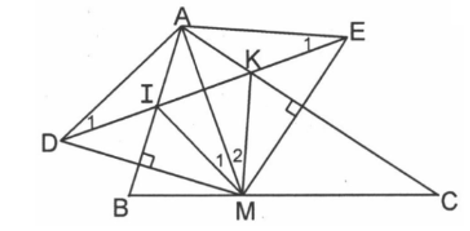
Cho tam giác ABC có , và là các góc nhọn, M là một điểm thuộc BC. Gọi D là điểm đối xứng với M qua AB, E là điểm đối xứng với M qua AC. Gọi I, K là giao điểm của DE với AB, AC.
a) Tính các góc của tam giác DAE.
Trả lời
a)
Ta có D là điểm đối xứng với M qua AB (giả thiết).
Suy ra AB là đường trung trực của đoạn DM.
Do đó AD = AM.
Vì vậy tam giác ADM cân tại A.
Suy ra AB vừa là đường trung trực, vừa là đường phân giác của tam giác ADM.
Do đó .
Chứng minh tương tự, ta được .
Ta có .
Ta có:
⦁ AB là đường trung trực của đoạn DM. Suy ra AD = AM.
⦁ AC là đường trung trực của đoạn EM. Suy ra AM = AE.
Do đó AD = AE.
Vì vậy tam giác ADE cân tại A.
Suy ra .
Vậy và .