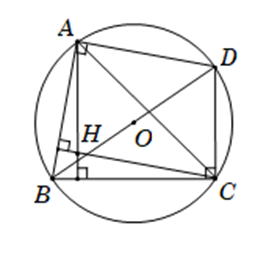
Cho tam giác ABC có trực tâm H. Gọi D là điểm đối xứng với B qua tâm O của đường tròn ngoại tiếp tam giác ABC. Khẳng định nào sau đây đúng?

A. \(\overrightarrow {HA} = \overrightarrow {C{\rm{D}}} ;\overrightarrow {A{\rm{D}}} = \overrightarrow {CH} \)

B. \(\overrightarrow {HA} = \overrightarrow {C{\rm{D}}} ;\overrightarrow {A{\rm{D}}} = \overrightarrow {HC} \)

C. \(\overrightarrow {HA} = \overrightarrow {C{\rm{D}}} ;\overrightarrow {AC} = \overrightarrow {CH} \)

D. \(\overrightarrow {HA} = \overrightarrow {C{\rm{D}}} ;\overrightarrow {A{\rm{D}}} = \overrightarrow {HC} ;\overrightarrow {OB} = \overrightarrow {O{\rm{D}}} \).

Đáp án đúng là: B

Vì tam giác ACD nội tiếp (O) nên tam giác BCD vuông tại C

Suy ra BC ⊥ CD

Mà AH ⊥ CB nên AH // DC

Vì tam giác ABD nội tiếp (O) nên tam giác BAD vuông tại A

Suy ra BA ⊥ AD

Mà CH ⊥ AB nên CH // DA

Xét tứ giác ADCH có AH // DC và CH // DA

Suy ra ADCH là hình bình hành

Do đó \(\overrightarrow {HA} = \overrightarrow {C{\rm{D}}} ;\overrightarrow {A{\rm{D}}} = \overrightarrow {HC} \)

Vậy ta chọn đáp án B.