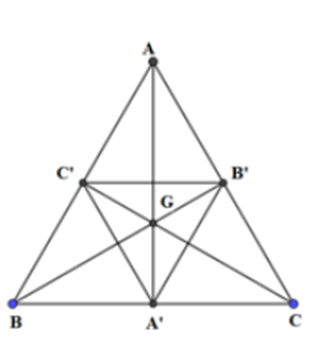
Cho tam giác ABC có trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm của các cạnh
Cho tam giác ABC có trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm của các cạnh BC, CA, AB. Phép vị tự tâm G biến tam giác ABC thành tam giác A’B’C’ có tỉ số vị tự bằng bao nhiêu?
A. \( - \frac{1}{2}\)
B. \(\frac{1}{2}\)
C. \(\frac{2}{3}\)
D. \( - \frac{1}{3}\).