Cho tam giác ABC, có M, N, K, I lần lượt là trung điểm của AB, AC, MB, MC.
a) Cho MN = 2,5 cm. Tính BC.
b) Chứng minh MNIK là hình bình hành.
c) Tam giác ABC cần điều kiện gì để MNIK là hình chữ nhật.
d) SABC = a. Tính SAMN theo a.
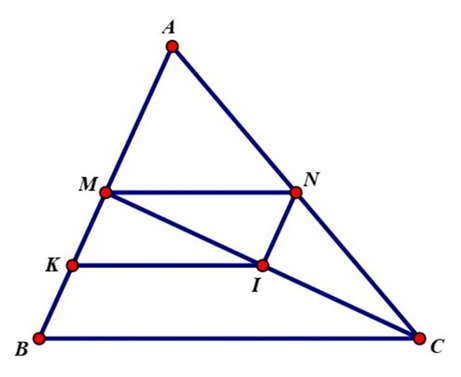
) Xét Δ ABC có:
M là trung điểm cạnh AB
N là trung điểm cạnh AC
⇒ MN là đường trung bình Δ ABC
⇒ MN = \(\frac{1}{2}\)BC và MN // BC (1)
⇒ BC = 2.MN = 2.2,5 = 5 cm.
b) ΔMBC có:
MK = KB (K trung điểm của MB)
MI = IC (I trung điểm của IC)
⇒ IK là đường trung bình ΔMBC, nên IK // BC và IK = \(\frac{1}{2}\)BC (2)
Từ (1), (2) suy ra MN // KI và MN = KI
⇒ Tứ giác MNIK là hình bình hành.
c) Ta có: tứ giác MNIK là hình bình hành (câu b). Để hình bình hành MNIK là hình chữ nhật thì \(\widehat {MKI} = 90^\circ \)
⇔ IK ⊥KM
⇔ IK ⊥ AB
⇔ BC ⊥ AB (vì IK // BC)
⇔ ΔABC vuông tại B.
d) Kẻ đường cao AH của tam giác ABC và AMN
Ta có: \(\frac{{{S_{ABC}}}}{{{S_{AMN}}}} = \frac{{\frac{1}{2}.AH.BC}}{{\frac{1}{2}.AH.MN}} = \frac{{BC}}{{MN}} = 2\)
⇒ SAMN = \(\frac{1}{2}\)SABC = \(\frac{a}{2}\).