Cho tam giác ABC có hai trung tuyến BD và CE cắt nhau tại G. Gọi M ,N theo thứ tự là trung điểm của BG và CG.

a, Chứng minh tứ giác MNDE là hình bình hành .

b, Tìm điều kiện của tam giác ABC để MNDE là hình chữ nhật.

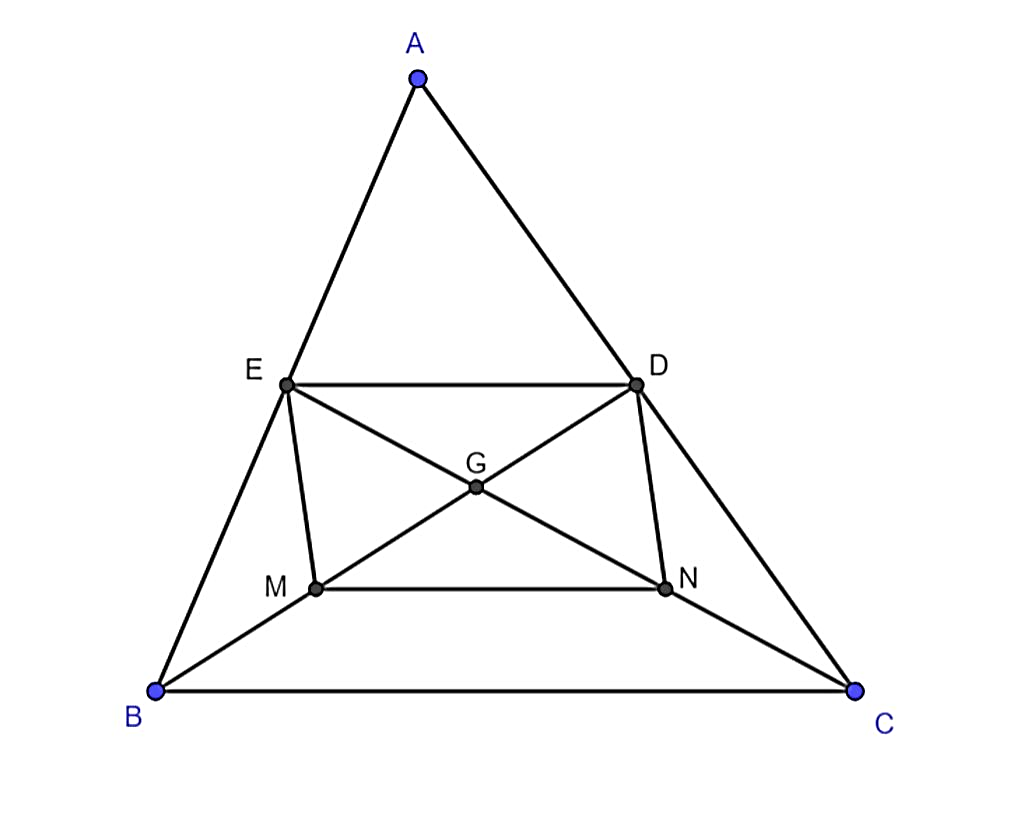
Xét tam giác ABC có AE = EB (gt), AD = DC (gt)

⇒ ED là đường trung bình của tam giác ABC

⇒ ED // BC và ED = $\frac{1}{2}$ BC

Xét tam giác BGC có BM = MG (gt), CN = NG (gt)

⇒ MN là đường trung bình của tam giác BGC

⇒ MN // BC và MN = $\frac{1}{2}$ BC

Có MN // BC mà ED // BC ⇒ MN//ED

MN = $\frac{1}{2}$ BC, ED = $\frac{1}{2}$ BC ⇒ MN = ED

Tứ giác MNDE có: MN // ED, MN = ED

⇒ MNDE là hình bình hành

b, Hình bình hành MNDE là hình chữ nhật

⇔ $\widehat{NDE}$ = 90°

Nếu $\widehat{NDE}$  = 90°

⇒ BD vừa là trung tuyến vừa là đường cao của tam giác ABC ứng với AC

⇒Tam giác ABC cân tại B

Vậy, để hình bình hành MNDE là hình chữ nhật, tam giác ABC phải cân tại B.