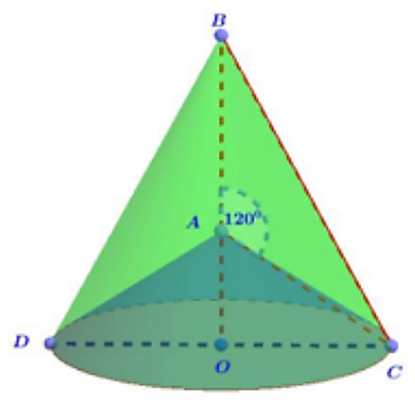
Cho tam giác ABC có góc A = 120 độ, AB = AC = a. Quay tam giác ABC
Cho tam giác ABC có \(\widehat A = 120^\circ ,\) AB = AC = a. Quay tam giác ABC (bao gồm điểm trong tam giác) quanh đường thẳng AB ta được một khối tròn xoay. Thể tích khối tròn xoay đó bằng:
A. \(\frac{{\pi {a^3}}}{3}.\)
B. \(\frac{{\pi {a^3}}}{4}.\)
C. \(\frac{{\pi {a^3}\sqrt 3 }}{2}.\)
D. \(\frac{{\pi {a^3}\sqrt 3 }}{4}.\)