Cho tam giác ABC có đường cao AD, và trực tâm H. Gọi I, K lần lượt là trung điểm của HA, HB. Gọi E, F lần lượt là trung điểm của BC, AC. Chứng minh

a) Bốn điểm E, F, I, K cùng thuộc một đường tròn.

b) Điểm D cũng thuộc đường tròn đi qua bốn điểm E, F, I, K.

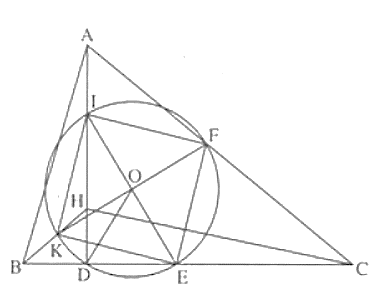
a) Ta có: IK là đường trung bình của tam giác ABH vì I, K là trung điểm HA, HB

⇒ IK // AB và IK = $\frac{1}{2}AB$

Tương tự: FE là đường trung bình của ∆ABC

⇒ FE // AB và FE = $\frac{1}{2}AB$

⇒ IK // FE và IK = FE

Nên IKEF là hình bình hành (1)

Giả sử giao điểm IE và KF là O

IF là đường trung bình của ∆AHC nên IF // HC

Lại có: IF ⊥ IK (2) (vì IF // HC, IK // AB, HC ⊥ AB)

Từ (1) và (2) suy ra: IKEF là hình chữ nhật.

Ta có: OE = OF = OI = OK nên bốn điểm E, F, I, K cùng nằm trên đường tròn (O; OE)

b) Tam giác IDE vuông tại D, DO là đường trung tuyến nên DO = OI = OE

Vậy D cũng nằm trên đường tròn (O; OE).