Cho tam giác ABC có BD, CE là các trung tuyến cắt nhau tại G.

a) Tứ giác BEDC hình gì ?

b) Gọi M, N lần lượt là trung điểm của BG và CG. Chứng minh tứ giác MEDN là hình bình hành.

c) Tam giác ABC có thêm điều kiện gì thì tứ giác MEDN là hình chữ nhật.

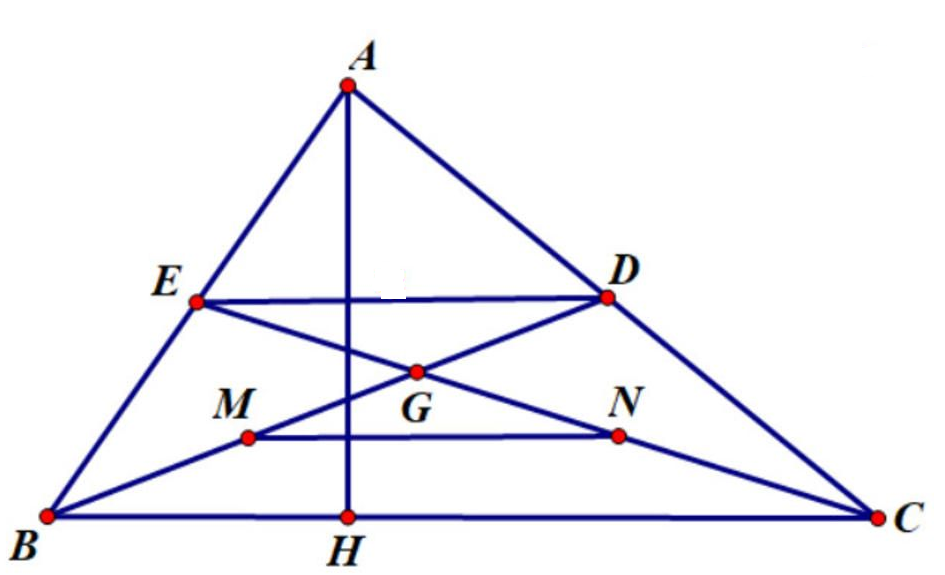
a) Tam giác ABC có E là trung điểm của AB, D là trung điểm của AC

⇒ ED là đường trung bình của tam giác ABC

⇒ ED // BC và ED = $\frac{1}{2}$ BC (1)

⇒ Tứ giác BEDC là hình thang

b) Tam giác GBC có M là trung điểm của GB,N là trung điểm của GC

⇒ MN là đường trung bình của tam giác GBC

⇒ MN // BC và MN = $\frac{1}{2}$ BC (2)

Từ (1), (2) ⇒ ED//MN và ED = MN

⇒ Tứ giác MEDN là hình bình hành

c) Tứ giác MEDN là hình chữ nhật

⇔ MEDN là hình bình hành có 2 đường chéo bằng nhau 

⇔ EN = DM

Mà EN = $\frac{2}{3}$  EC, DM = $\frac{2}{3}$ DB

⇒ EC = BD

Hình thang BEDC có EC = BD

⇒ BEDC là hình thang cân ⇒ $\widehat{EBC}=\widehat{DCB}$

⇒ Tam giác ABC cân tại A 

Vậy tam giác ABC cân tại A thì tứ giác MEDN là hình chữ nhật.