Cho tam giác ABC có AB = AC. Tia phân giác của góc A cắt BC tại D.                                         

a) Chứng minh tam giác ABD bằng tam giác ADC.                                                                

b) Kẻ DH vuông góc với AB (H thuộc AB), DK vuông góc với AC (K thuộc AC). Chứng minh DH = CK.                                                       

c) Biết $\widehat{A}$ = 4$\widehat{B}$ , tính số đo các góc của tam giác ABC.

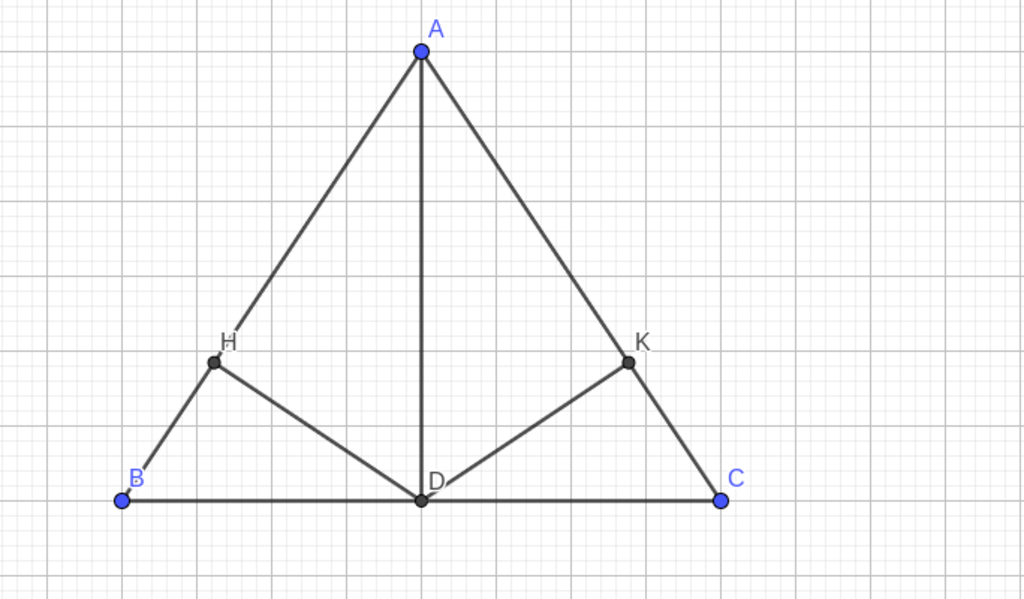
a) Ta có: AB = AC, $\widehat{BAD}=\widehat{DAC}$

Xét ∆ABD và ∆ACD có:

AB = AC

$\widehat{BAD}=\widehat{DAC}$

Chung AD

⇒∆ABD = ∆ACD (c.g.c)

b) Từ câu a suy ra: DB = DC

Mà $\widehat{DHB}=\widehat{DKC}=90°$ , $\widehat{ABC}=\widehat{ACB}$ (vì tam giác BAC cân tại A)

Xét ∆DHB và ∆DKC có: $\widehat{DHB}=\widehat{DKC}=90°$

DB = DC

$\widehat{DBH}=\widehat{DCK}$

⇒∆DHB = ∆DKC (g.c.g)

⇒ BH = CK

c) Ta có: $\widehat{ABC}=\widehat{ACB}$

 Mà $\widehat{A}$ = 4$\widehat{B}$  nên: $\widehat{A}+\widehat{B}+\widehat{C}=4\widehat{B}+\widehat{B}+\widehat{B}=180°$

⇒ $\widehat{B}=180°:6=30°$ ⇒ $\widehat{C}=30°$

$\widehat{A}=4\widehat{B}=4.30°=120°$.