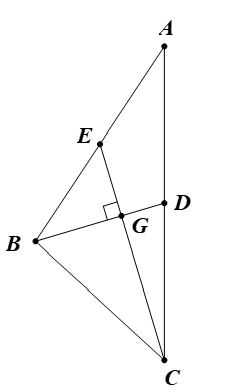
Ta có D, E lần lượt là trung điểm của AC, AB.

Suy ra $BE=\frac{AB}{2}=3\left(cm\right);CD=\frac{AC}{2}=4\left(cm\right)$ .

Gọi G là giao điểm của CE và BD.

Suy ra G là trọng tâm của tam giác ABC.

Đặt GD = x, GE = y.

Áp dụng tính chất trọng tâm cho tam giác ABC, ta được:

⦁ $GD=\frac{1}{2}BG$ . Suy ra BG = 2GD = 2x.

⦁ $GE=\frac{1}{2}CG$ . Suy ra CG = 2GE = 2y.

Áp dụng định lí Pitago cho tam giác BGE vuông tại G: BG² + GE² = BE².

⇔ 4x² + y² = 9 (1)

Áp dụng định lí Pitago cho tam giác CGD vuông tại G: CG² + GD² = CD².

⇔ 4y² + x² = 16 (2)

Lấy (1) + (2) vế theo vế, ta được 5(x² + y²) = 25.

⇔ x² + y² = 5.

Áp dụng định lí Pitago cho tam giác BGC vuông tại G: BG² + CG² = BC².

⇔ 4x² + 4y² = BC².

⇔ 4(x² + y²) = BC².

⇔ BC² = 4.5 = 20.

Vậy $BC=2\sqrt{5}\left(cm\right)$ .