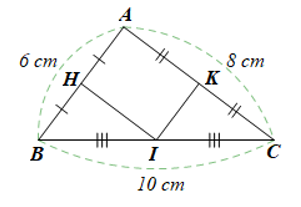
Cho tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 10 cm. Gọi H, I, K lần lượt là trung điểm của AB, BC, AC. Chu vi của tứ giác AHIK bằng

A. 7 cm.

B. 14 cm.

C. 24 cm.

D. 12 cm.

Đáp án đúng là: B

Ta có: BC2 = 102 = 100, AB2 + BC2 = 62 + 82 = 36 + 64 = 100

Suy ra BC2 = AB2 + BC2

Do đó, ∆ABC vuông tại A (định lý Pythagore đảo).

Trong ∆ABC có:

• H, I lần lượt là trung điểm của AB và BC nên HI là đường trung bình của ∆ABC;

Suy ra HI // AC và $HI=\frac{1}{2}AC$ (tính chất đường trung bình trong tam giác)

Hay $HI=\frac{1}{2}\cdot 8=4$ (cm).

• I, K lần lượt là trung điểm của BC và AC nên IK là đường trung bình của ∆ABC

Suy ra IK // AB và $IK=\frac{1}{2}AB$ (tính chất đường trung bình trong tam giác)

Hay $IK=\frac{1}{2}\cdot 6=3$ (cm).

Ta có ∆ABC vuông tại A nên AB ⊥ AC, mà HI // AC nên AB ⊥ HI

Lại có IK // AB nên HI ⊥ IK tại I

Tứ giác AHIK có: $\widehat{HAK}=\widehat{IHA}=\widehat{IKA}=90°$ nên AHIK là hình chữ nhật.

Chu vi của tứ giác AHIK bằng: 2.(IH + IK) = 2.(4 + 3) = 14 (cm).