Cho tam giác ABC có AB = 2, AC = 3, góc BAC = 60^0. Gọi M là trung điểm của đoạn thẳng BC. Điểm D thỏa mãn vecto AD = 7/12 vecto AC. a) Tính vecto AB. vecto AC. b) Biểu diễn vecto AM, vect
32
24/07/2024
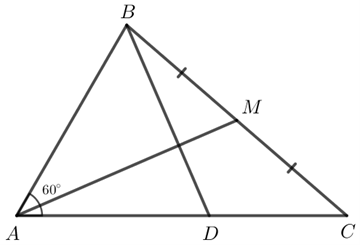
Cho tam giác ABC có AB = 2, AC = 3, \[\widehat {BAC} = 60^\circ \]. Gọi M là trung điểm của đoạn thẳng BC. Điểm D thỏa mãn \(\overrightarrow {AD} = \frac{7}{{12}}\overrightarrow {AC} \).
a) Tính \(\overrightarrow {AB} .\overrightarrow {AC} \).
b) Biểu diễn \(\overrightarrow {AM} ,\,\overrightarrow {BD} \) theo \(\overrightarrow {AB} ,\overrightarrow {AC} \).
c) Chứng minh AM ⊥ BD.
Trả lời
Lời giải
a) Ta có \(\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\)
\( = AB.AC.\cos \widehat {BAC} = 2.3.\cos 60^\circ = 3\).
Vậy \(\overrightarrow {AB} .\overrightarrow {AC} = 3\).
b) Do M là trung điểm của BD nên \(\overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} \).
Ta có \(\overrightarrow {BD} = \overrightarrow {AD} - \overrightarrow {AB} = \frac{7}{{12}}\overrightarrow {AC} - \overrightarrow {AB} \).
Vậy \(\overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} \) và \(\overrightarrow {BD} = \frac{7}{{12}}\overrightarrow {AC} - \overrightarrow {AB} \).
c) Ta có \(\overrightarrow {AM} .\overrightarrow {BD} = \left( {\frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} } \right)\left( {\frac{7}{{12}}\overrightarrow {AC} - \overrightarrow {AB} } \right)\).
\( = \frac{7}{{24}}\overrightarrow {AB} .\overrightarrow {AC} - \frac{1}{2}{\overrightarrow {AB} ^2} + \frac{7}{{24}}{\overrightarrow {AC} ^2} - \frac{1}{2}\overrightarrow {AB} .\overrightarrow {AC} \).
\( = - \frac{5}{{24}}\overrightarrow {AB} .\overrightarrow {AC} - \frac{1}{2}A{B^2} + \frac{7}{{24}}A{C^2}\).
\( = - \frac{5}{{24}}.3 - \frac{1}{2}{.2^2} + \frac{7}{{24}}{.3^2} = 0\).
Vậy AM ⊥ BD.

