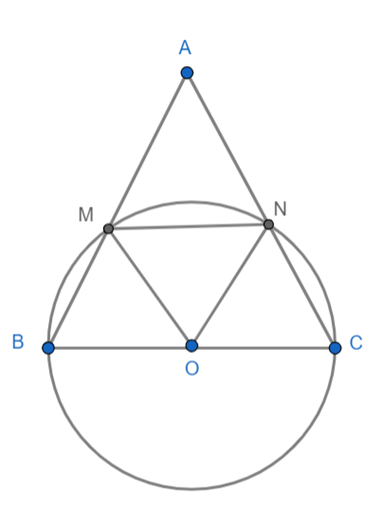
cho tam giác ABC cân tại A. Vẽ đường tròn tâm O, đường kính BC. Đường tròn (O) cắt AB và AC lần lượt tại M và N.
a) Chứng minh các cung nhỏ BM và CN có số đo bằng nhau.
b) Tính \(\widehat {MON}\) biết \(\widehat {BAC} = 40^\circ \).
a) Ta có OM = OB = ON = OC
Suy ra ∆OBM và ∆OCN cân tại O mà ABC cân tại A nên \(\widehat {ABC} = \widehat {ACB}\)
Xét ∆OBM và ∆OCN có:
OM = ON
\(\widehat {MBO} = \widehat {NCO}\)
BO = OC
Suy ra: ∆OBM = ∆OCN (c.g.c)
Suy ra: \(\widehat {MOB} = \widehat {NOC}\)(đpcm)
b) Vì ABC cân tại A nên \(\widehat {ABC} = \widehat {ACB} = \left( {180^\circ - 40^\circ } \right):2 = 70^\circ \)
nên \(\widehat {MOB} = \widehat {NOC} = 70^\circ \)
\(\widehat {MON} = 180^\circ - \left( {\widehat {MOB} + \widehat {NOC}} \right) = 180^\circ - \left( {40^\circ + 40^\circ } \right) = 100^\circ \).