Bài 3 trang 82 Toán 7 Tập 2:
Cho tam giác ABC cân tại A. Tia phân giác của các góc B và C cắt nhau tại M. Tia AM cắt BC tại H. Chứng minh rằng H là trung điểm của BC.
|
GT |
ABC cân tại A, BM, CM lần lượt là tia phân giác của góc B và C, Tia AM cắt BC tại H. |
|
KL |
H là trung điểm của BC. |
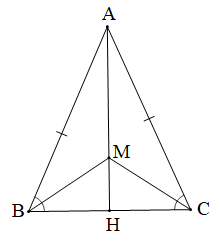
Tam giác ABC có tia phân giác của các góc B và C cắt nhau tại M (giả thiết)
Mà ba đường phân giác của tam giác đồng quy tại một điểm nên AM là đường phân giác của góc A của tam giác ABC.
Suy ra hay
Tam giác ABC cân tại A (giả thiết) nên AB = AC và
Xét tam giác ABH và tam giác ACH có:
(chứng minh trên);
AB = AC (chứng minh trên);
(chứng minh trên).
Do đó ∆ABH = ∆ACH (g.c.g)
Suy ra BH = CH (hai cạnh tương ứng)
Vậy H là trung điểm của BC.
Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:
Bài 7: Tính chất ba đường trung tuyến của tam giác
Bài 8: Tính chất ba đường cao của tam giác
Bài 9: Tính chất ba đường phân giác của tam giác
Bài 10: Hoạt động thực hành và trải nghiệm. Làm giàn hoa tam giác để trang trí lớp học