Cho tam giác ABC cân tại A. Kẻ đường trung tuyến AM. Tia phân giác của góc B cắt AM tại I
721
30/11/2023
Bài 2 trang 82 Toán 7 Tập 2:
Cho tam giác ABC cân tại A. Kẻ đường trung tuyến AM. Tia phân giác của góc B cắt AM tại I. Chứng minh rằng CI là tia phân giác của góc C.
Trả lời
|
GT
|
ABC cân tại A,
Trung tuyến AM,
Tia phân giác của góc B cắt AM tại I.
|
|
KL
|
CI là tia phân giác của góc C.
|
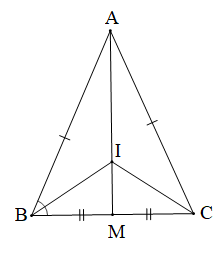
+) Tam giác ABC cân tại A (giả thiết) nên AB = AC.
Lại có AM là đường trung tuyến (giả thiết) do đó MB = MC (M là trung điểm của BC)
Xét ∆ABM và ∆ACM có:
AB = AC (chứng minh trên),
AM là cạnh chung,
MB = MC (chứng minh trên)
Do đó ∆ABM = ∆ACM (c.c.c)
Suy ra (hai góc tương ứng)
Suy ra AM là tia phân giác của
+) Tam giác ABC có AM, BI là hai đường phân giác cắt nhau tại I
Mà ba đường phân giác của tam cắt nhau tại một điểm nên I là giao điểm ba đường phân giác này.
Do đó CI là tia phân giác của góc C.
Vậy CI là tia phân giác của góc C.
Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:
Bài 7: Tính chất ba đường trung tuyến của tam giác
Bài 8: Tính chất ba đường cao của tam giác
Bài 9: Tính chất ba đường phân giác của tam giác
Bài 10: Hoạt động thực hành và trải nghiệm. Làm giàn hoa tam giác để trang trí lớp học
Bài tập cuối chương 8
Câu hỏi trang 85 Toán 7 Tập 2

