Cho tam giác ABC cân tại A, góc BAC = 120 độ  và AB = 4 cm.

Trả lời

Áp dụng định lí cosin trong tam giác ABC, ta có: 

$B{C}^2=A{B}^2+A{C}^2-2AB.AC.\cos \widehat{BAC}$

$=4^2+4^2-2.4.4.\left(\frac{-1}{2}\right)=48$

$\Rightarrow BC=4\sqrt{3}$

Gọi H là trung điểm của BC.

Khi quay tam giác ABC quanh cạnh BC ta được 2 hình nón có chung bán kính đáy AH, đường cao lần lượt là BH và CH với:

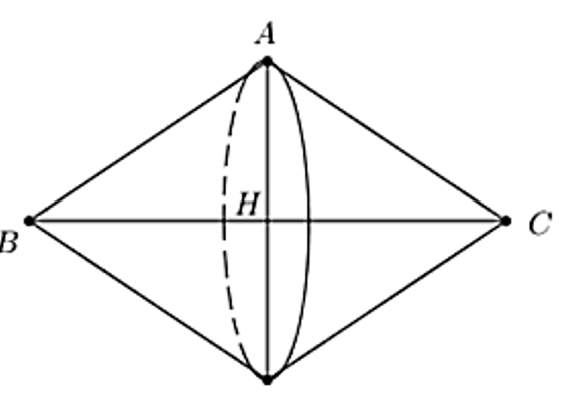
AH = AB.cos 60° = 2 

$BH=CH=\frac{1}{2}BC=\frac{4\sqrt{3}}{2}=2\sqrt{3}$

$V=\frac{1}{3}\pi .A{H}^2.BH+\frac{1}{3}\pi .A{H}^2.CH$

$=\frac{1}{3}\pi .A{H}^2.\left(BH+CH\right)$

$=\frac{1}{3}\pi .2^2.\left(2\sqrt{3}+2\sqrt{3}\right)=\frac{16\pi \sqrt{3}}{3}$

Khi quay tam giác ABC quanh AB ta được khối tròn xoay như sau:

Gọi D là điểm đối xứng C qua AB, H là trung điểm của CD.

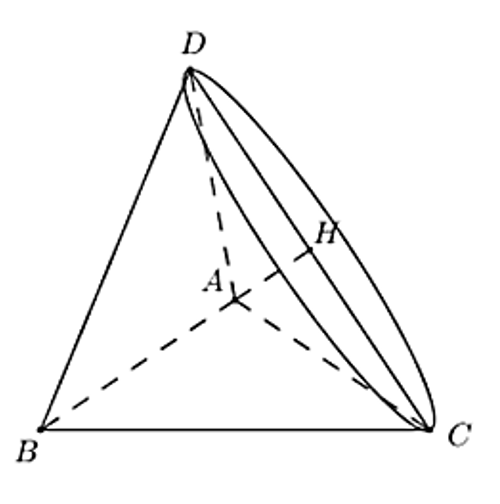
Ta có:  $\widehat{ABC}=\frac{180°-120°}{2}=30°$

$\Rightarrow HC=BC.\sin 30°=4\sqrt{3}.\frac{1}{2}=2\sqrt{3}$

$BH=BC.\cos 30°=4\sqrt{3}.\frac{\sqrt{3}}{2}=6$

$\Rightarrow V=\frac{1}{3}\pi .H{C}^2.BH-\frac{1}{3}\pi .H{C}^2.AH$

$=\frac{1}{3}\pi .H{C}^2.AB=\frac{1}{3}\pi .{\left(2\sqrt{3}\right)}^2.4=16\pi$

Do điểm B và C có vai trò như nhau nên khi quay tam giác ABC quanh AC ta cũng nhận được khối tròn xoay có thể tích bằng 16p.

Vậy thể tích lớn nhất có thể được khi quay tam giác ABC quanh một đường thẳng chứa cạnh của tam giác ABC là 16π.