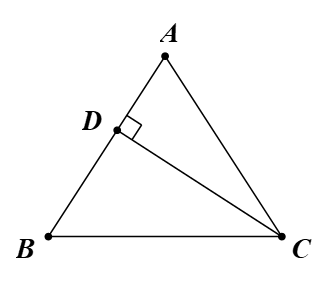
Áp dụng định lí Pytago cho tam giác ACD vuông tại D: AD² + CD² = AC²   (1)

⇔ AD² + CD² = AB² (do tam giác ABC cân tại A nên AB = AC)    (2)

Áp dụng định lí Pytago cho tam giác DBC vuông tại D: BD² + CD² = BC²    (3)

Lấy (1) + (2) + (3) vế theo vế, ta được: BD² + 2AD² + 3CD² = AB² + BC² + AC².

Vậy ta có điều phải chứng minh.