Cho tam giác ABC biết độ dài ba đường trung tuyến lần lượt bằng 15, 18, 27.

a) Tính diện tích tam giác ABC.

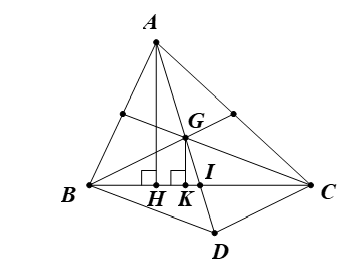
a) Gọi I là trung điểm BC và G là trọng tâm của tam giác ABC.

Suy ra $\frac{AI}{GI}=3$ .

Kẻ AH ⊥ BC và GK ⊥ BC (H, K ∈ BC).

Suy ra AH // GK.

Áp dụng định lí Thales, ta được: $\frac{AH}{GK}=\frac{AI}{GI}=3$ .

Khi đó $\frac{S_{ABC}}{S_{GBC}}=\frac{\frac{1}{2}.AH.BC}{\frac{1}{2}.GK.BC}=\frac{AH}{GK}=3$ .

Suy ra S_ABC = 3S_GBC.

Lấy D là điểm đối xứng với G qua I.

Suy ra I là trung điểm của GD.

Khi đó tứ giác BGCD là hình bình hành.

Suy ra $S_{GBC}=S_{BGD}=\frac{1}{2}{S}_{BGCD}$  .

Do đó S_ABC = 3S_BGD.

Giả sử m_a = 15, m_b = 18, m_c = 27.

Suy ra $\left\{\begin{array}{l}BG=\frac{2}{3}.m_b=\frac{2}{3}.18=12\\ BD=CG=\frac{2}{3}.m_c=\frac{2}{3}.27=18\end{array}\right.$

Ta có I là trung điểm của GD.

Suy ra . $GD=2GI=2.\frac{1}{3}AI=\frac{2}{3}.m_a=\frac{2}{3}.15=10$

Nửa chu vi của tam giác BGD là: $p=\frac{GD+BD+BG}{2}=\frac{10+18+12}{2}=20$ .

Diện tích của tam giác BGD là: $S_{BGD}=\sqrt{p\left(p-BG\right)\left(p-GD\right)\left(p-BD\right)}=40\sqrt{2}$ .

Suy ra $S_{ABC}=3S_{BGD}=3.40\sqrt{2}=120\sqrt{2}$ .

Vậy diện tích tam giác ABC bằng $120\sqrt{2}$ .